20:24 08/11/09
アルゴリズムコンテストの挑み方 (3)
TopCoderのAlgorithm部門や、Google Code Jamや、ACM/ICPC のような、 短時間でアルゴリズミックなコードを書くコンテストに挑むときに私が考えていることシリーズ。 第1回(書く前に実行時間を見積もる)、 第2回(問題をひとまわり小さくしてみる) の続きです。
第3回、なんでも"グラフ"にしてみる!
まえがき
グラフといっても棒グラフや円グラフのことではなくて、 グラフ理論 という分野のお話です。 実に様々なアルゴリズムがこの分野で作られていて、上にあげたコンテストでも、 グラフアルゴリズムで解ける問題がちょくちょく登場します。
…といっても今回は、その "様々なアルゴリズム" の細かい中身をお話しするつもりはありません。 その辺りは本やらWebやらで適宜情報仕入れてください。 どっちかというと、「いかにしてそういうアルゴリズムを使える状況に持ち込むか」 がテーマです。
(※ 参考までに、グラフ理論の解説書としては
『最短経路の本 / レナのふしぎな数学の旅』
が私オススメです。みんな読むべし読むべし。)
(※ お勉強したくない人向けの手抜き作戦としては…ぶっちゃけ、
ダイクストラ法 と
クラスカル法 の2つだけ使えれば8割方のグラフ問題に対応できるような気がします。
この2つも実装の詳細まで覚えてなくても、"どんな問題を解くアルゴリズムなのか" だけ把握してれば
「ググってコピペ」 「教科書を写経」「(使っていいコンテストなら)ライブラリ探してきちゃう」
でどうにかならなくもないでしょう。えーと、ダイクストラ法は「ある点から別の点への最短経路」を求める方法で、
クラスカル法は…どう説明しよう…ドラクエで言うと「無限にルーラが使える (= 一度行った街には0歩で戻れる)
ときに全部の街を訪れる最短経路」かな。ちょっと違うか。
もちろん、ちゃんと詳細を理解するに超したことはないわけですが…。)
まあ、でも、大したことはありません。問題を見たらとりあえずグラフ化してみよう、 というだけです。方程式の解の公式を使える状況に持ち込むは、まず方程式を立てなきゃいけないのと同じです。 グラフのアルゴリズムを使うにはまずグラフを作らないといけません。 とても当たり前なように聞こえますが、実際にコンテストをやってみると、なかなかどうして、 見落としがちなところです。
ウォームアップ
「問題: ある都市の路線図(駅のリストと駅と駅の接続・距離情報)が入力されたときに、 A駅からB駅までの最短経路を求めましょう」
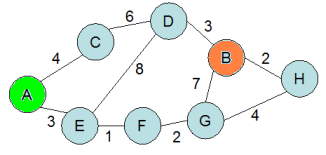 グラフというのは要するに、
左の図のようないくつかの「丸/点」とそれを繋ぐ「線」でできてる図のことを言います。
とにかく問題を見たらこの「点と線」の形で描いてみましょう!
というのがポイントです。
グラフというのは要するに、
左の図のようないくつかの「丸/点」とそれを繋ぐ「線」でできてる図のことを言います。
とにかく問題を見たらこの「点と線」の形で描いてみましょう!
というのがポイントです。
今回の場合は変な工夫を凝らす必要はなにもなくて、各「駅」を「点」にして、 路線で隣り合ってる駅と駅の間に「線」を引いてみます。左の図は、 「A駅からC駅が4km、C駅からD駅が6km、…」という情報をグラフで描いてみたものです。 (単位はkm)
ダイクストラ法 というアルゴリズムを使うと、 「線に"距離"という付加情報が乗ってるグラフ」 での指定した点から点までの最短経路を求めることができます。 のでこの問題はそれで解決。 参考として、id:mokehehe さんの 実際の東京の路線データでダイクストラ法してみる という記事が面白かったです。
応用例 : 時刻表
もーちょいリアルな問題設定を考えてみましょうか。 「ある都市の路線図と、各路線の時刻表がデータとして与えられます。 8:00にA駅を出発して最速でB駅に着く経路を見つけてください」
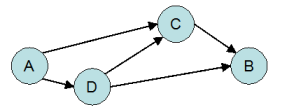
ほげ線(上り) A -> C -> B 7:45 8:25 8:45 8:00 8:40 9:00 8:15 8:55 9:15 ふが線(上り) ぴよ線(上り) A -> D -> B D -> C 8:00 8:05 9:10 8:07 8:22 8:20 8:25 9:30 8:20 8:35 8:40 8:45 9:50 8:33 8:48
今度は、単純に駅と接続関係だけからグラフを作ろうとすると、 「時刻表」の情報が抜け落ちてしまいます。 線に「時刻表」の情報を付加情報として乗っけてグラフと見なすことはできなくはないですが、 そういうグラフを作っても既存のアルゴリズムを適用することができません。 ダイクストラ法が扱える付加情報は"距離"と"向き"だけですし、 他のアルゴリズムでも、扱う付加情報はせいぜい(線をネットワーク接続と見なして)"回線容量" くらいです。
繰り返します。グラフのアルゴリズムを適用するには、 線には"距離"か"向き"か"容量"程度の情報しか乗せられません。 でもなんとかして無理矢理時刻表の情報を乗せてグラフを作りたい。どうしましょう。 そう、線には"距離"しか乗せちゃいけないなら、点の方に乗せればいいじゃない!
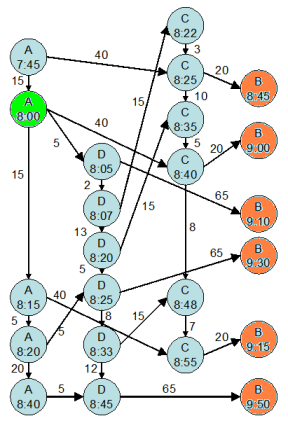
(駅,時刻) のペアを「点」にして、点から点へ動けるようなところに「線」を、 何分かかるかの情報を添えてグラフにしました。同じ駅の違う時刻には、時刻の差の分だけ時間をかければ移れるので、 そういう線を引いてあります。 こうすると、問題が 「点」と「線」と「線に乗せた"距離"(この場合は時間的な"距離"ですね)情報」 というグラフの形に描けました。 一度グラフにさえしてしまえば、もうこっちのもの。 「A 8:00 という点」から「B ?:?? という点のどれか」への最短経路は、 ダイクストラ法一発で計算終了です。ウォームアップの問題と解き方はまったく同じ。
「ダイクストラ法 == 最短距離/最短経路」と考えていると、 地理的なオブジェクト(駅とか)をそのまま「点」にしてグラフを作ることしか思い浮かばなくなってしまいがちです。 これは、たぶん、発想としては逆の方がよいと思う。 できるだけ「点」に入力の情報を突っ込んでとにかくグラフ化してみる。 で、いったんグラフを作ってから、「元々の問題で求めたかった答えは、 このグラフで言うと何を求めることになるんだろう?」と考えてみる。 そこで「このグラフで言うと最短経路だ!」ということになったら、 そこで初めてダイクストラ法のことを思い出す。
応用例 : コイン再び
前回の例題を再掲します。
『Anarchygolfania という国で流通している貨幣(コイン)の一覧と、 払いたい金額が与えられます。
できるだけコインの枚数が少なくなる払い方を答えましょう』です。
たとえば、Anarchygolfania には1円玉と7円玉と12円玉だけがある場合、14円を払うには、
7円玉2枚で払うのが最適です。
 前回は「パラメータを1つ小さくしてみる」方法で解きましたが、
それは忘れて今回の流儀でもう一度考えてみます。そう、「問題を見たらグラフにしてみる」。
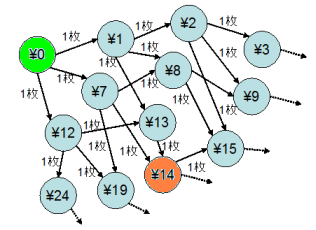
「払った金額」を点に、1枚コインを追加すると払えるところに線を引くと、右図のようなグラフになります。
元々求めたかったもの…「14円を払う最適な払い方」は、
グラフで言うと「点"\0"から点"\14"への最短経路」に他なりません。ダイクストラ法の出番です。
前回は「パラメータを1つ小さくしてみる」方法で解きましたが、
それは忘れて今回の流儀でもう一度考えてみます。そう、「問題を見たらグラフにしてみる」。
「払った金額」を点に、1枚コインを追加すると払えるところに線を引くと、右図のようなグラフになります。
元々求めたかったもの…「14円を払う最適な払い方」は、
グラフで言うと「点"\0"から点"\14"への最短経路」に他なりません。ダイクストラ法の出番です。
(※ 全部の線の距離が"1枚"と等しいので、 実際にはダイクストラ法よりもっと効率的に最短経路は求まります(前回の解法その3です)。 ただまあ、いちいち考え分けるの面倒くさいから全部ダイクストラでもいいよね、みたいな…。)
まとめ?
かなり慣れていれば 「じっと問題を睨んでグラフ問題っぽいと閃いたらグラフを作り始める」 でも良いかもしれないんですが、それはなかなか難しいのではないかと思います。 とにかく「まずは何も考えず"点と線"の形で問題を描いてみる」というのが自分のやり方その2です。 上の3つの例みたいに、グラフとして整理すればすぐ全部同じ「最短経路」の問題と判明することも多いですし、 何か解法を閃こうとするのはその後。 どうにもグラフっぽくならなければ(or 線に変に情報が乗りまくるグラフしか作れなければ)、諦める。
