Derive Your Dreams

19:27 08/02/29

不動点ふたたび

LtU で "Data Types a la Carte" を読みました。これの鍵となる技は「型コンストラクタに対する不動点演算子」だと思うのだけど、 あれ、なんで俺これ考えたことなかったんだ…？と不思議に思うくらい楽しげなアイデアですね。てい。

// 不動点演算子 via テンプレート。Dで。
//
// Haskell でいう"普通の"不動点関数 fix f = f (fix f) と同じようなもの
// = の代わりに継承になっちゃってますけど、まあ似たようなものです

class Fix!(alias F) : F!(Fix!(F)) {}

不動点演算の実装は本題ではないので、Yコンビネータみたいな無駄な複雑化はしない方針で。 さて、これを使って

class Pair(T)
{
    T left;
    T right;
}

２個同じ型の値のペアを保存するPair型のテンプレートの不動点を取ると

alias Fix!(Pair) Tree;

Tree t = new Tree;
t.left = new Tree;
t.left.left = new Tree;
t.left.right = new Tree;
t.right.left = new Tree;
...
t.left.right.right.right.left.right.right.left.right.left.left.right.left.left = null;

なんとびっくり、二分木になりました！

「型 X が Pair の不動点である」＝＝「型 X と 型 Pair!(X) が同じ物」で、 型 Pair!(X) の定義は「X型のメンバleftとX型のメンバrightを持ってるクラス」だったので、合わせると 「型 X は X型のメンバleftとX型のメンバrightを持ってるクラス」という結論が導かれるわけです。

以下蛇足

むかし、再帰関数をわざわざ不動点演算子で定義するのに何か意味があるとするなら、 アスペクトというかデコレータというか、処理を挟み込むフレームワークとしてでは…とかなんとか考えたことが あるのですが、同じことをここでも考えてみよう。上の例の、木の構造だけを持っている 単純なTreeを、ノードにタグ名をつけられるようにデコレートしてみる。

class TagFix!(alias F) : F!(TagFix!(F))
{
    string tag;
}

alias TagFix!(Pair) TagTree;
TagTree t = new TagTree;
t.tag = "html";
t.left = new TagTree;
t.left.tag = "head";
t.right = new TagTree;
t.right.tag = "body";

できた！Pairの定義に手を加えずに！ いやまあ、やってることだけ見ると、継承して tag っていうメンバを増やしてるだけなんですが。 でも考えてみよう。もし元々の Tree の定義が Fix!(Pair) じゃなくて、もっと素直な定義だったら。

class Tree
{
    Tree left;
    Tree right;
}

class TagTree : Tree
{
    string tag;
}

これでは、さっきのコードが通らない。

TagTree t = new TagTree; // ok
t.tag = "html";          // ok
t.left = new TagTree;    // ok
t.left.tag = "head";     // 型エラー!! t.leftの型はTree。TagTreeじゃない

これができたりするのが、無駄に型に不動点を使ってみた場合の面白いところです。 再帰関数をメモ化するときは、ちゃんと中の再帰呼び出しでもメモ化版を呼んでくれないと困る、 というのと同じ現象ですね。 相互再帰する型の不動点をとる演算子を実装するのもたいした手間じゃないので、 Graph の Node と Edge と ColoredNode と WeightedEdge と みたいな再帰に応用することもできなくもないかも。

蛇足の蛇足

なお、TagTree::leftの型が～というのは、不動点演算を使ったことで生じる利点ではなくて、 単純に再帰を使ったことによる利点でしかありません。つまり要するに Curiously recurring template pattern なのだけど、汎用のFixを使うとむしろFirewallとしての効果が微妙になるような気すらしないでもない。 外からデコレーションを追加できるというのは、これも型をパラメタライズしたことの利点であって、 つまり要するにただの Policy Based Design の亜種なのであった。

というわけで、「以下蛇足」の節は実はぜんぜん不動点関係ないということに書き終わってから気づいたけど 消すのももったいないので残してあるだけなのでした。そこんとこ注意。

ポイントは前半にあって、Pair(もどき) というそこらにありそうなテンプレートに Fix を適用したら 何故か二分木になっちゃったように、普通にそこら辺に転がっているテンプレートの不動点を取ってみると実は結構楽しいのではないかと思うのです。list とか vector とか。 線形コンテナはだいたい全部木になるのかな。で、そういう遊びを経由して作ったものを使うときに、 「蛇足」のようなデコレーション技が効いてくるんじゃないかなーと思います。

18:32 08/02/28

アルゴリズムクイズを作る

ACM-ICPC の世界大会に行くチームに集まってもらって 強化合宿をやったりだとか、予選の一週間前に練習コンテスト開いたりだとか、そういうことを やってる集団がありまして、そのイベントで使うために、 色々問題を作ったりします。

自分の場合問題の作り方は大きく分けて２通りあって、

名前駆動

なんだか知らないが先に問題の名前が思い浮かぶので、それに合わせて問題内容を考える。 先に問題の名前が～というのはつまり要するにダジャレだったりなんだったりするんですが。

"Eight Princes" はその年の大会会場が八王子だったのでつい。 当然 エイトクイーン が強く連想される名前なので、それっぽく、 お互い配置に干渉し合う王子様達の配置パターンを数えよう問題。 "Square Route" は名前から問題を思いつくまではすぐだったのだけど、そこから何とかして√っぽさを 出したいという理由で必死に考えた結果ナナメ45度線 （√2っぽい気がする！）という解法を導出。 "Divisor is the Conqueror" はなにかすごくよくあるアルゴリズムっぽい名前なのに全然そのアルゴリズム関係ないという 問題を作りたかったのだった。被害者は分割統治法です。

アルゴリズム駆動

も一つが、知ってるアルゴリズムを一個決めて「これを使って解ける問題を作ろう」とするパターン。 ただ、教科書から書き写せばすぐ解けるようでは面白くない。 「そのアルゴリズムがどういう原理で動いてて、どういうデータに対してまで一般化できるのか」 みたいなことを把握した上でアルゴリズムを変形できるようでないと解けないようにしたい。 "The Closest Circles"（この記事の１番近い円はど～れ？問題） や、"Magical Dungeon" などなどがこのパターンですね。

で

あとは、日常生活しててこれプログラムで解きたいなーと思った疑問を問題にしてみるとか。 ただ、自分の場合、たいてい極端に簡単か極端に難しくなっちゃってあんまり丁度よくならなかったりしますね。

それはいいんですけど、ICPCの過去問を見てたり、ひとのTopCoder日記を見てたりすると、 オリジナリティあふれた「どうやって思いつくんだこんな問題！」っていうのを結構見かけるんですよね。 それは何か名のついたアルゴリズムの変形なわけでも、当然ながら名前がダジャレなわけでもない。 そういう絶妙な難易度の問題をコンスタントに作れる人って言うのは、一体何駆動で問題を思いついているのだろう。 単純に引き出しの差だろうか。アルゴリズム駆動に近いんだけれど、私がそれに気づけるだけの 実力に達していない、というのは大いにあり得る。気になる。

17:26 08/02/25

D言語BOF(再掲)

D言語BOF :: 3月1日(土) 10:15 - 12:00

プログラムだいぶ固まってきたみたいです。発表者多数につき、 当初の予定より前に枠を拡大して「広い話（前半）」「濃い話（後半）」になるそうな。 当日参加できますが、申込数に応じて部屋（の大きさ）が変わるらしいので両方聴きたい方は 両方登録お願いします、とのことです。

私はいつものようにというかなんというか、適当にざっくり言語紹介する係をやることにしました。 前半組のみなさん綺麗な絵が出る面々が揃っていて、地味なことをやったらいけないような気がしてきた……

いろいろ

全問制覇 おめでとうございます！ 追いつけなかったー！

78 は、自分がずーっと1000万で割れる数を探すコードをいじくり回していたことに気づいたその瞬間に解決しました。 これはひどい。そして奇しくも 78×2＝156 が最後の１問になりそうな 雰囲気が漂って参りました。

Parsing Techniques をボチボチ読んでます。まだまだ最初の方なのですが [PDF] CFG構文解析と行列乗算 のアルゴリズムに関係がある、という話などなど面白い。

18:35 08/02/22

.bib 管理

論文で引用する参考文献のリストは BibTeX の .bib ファイルで書くわけですが。 これまで長らく手で書いたりコピペしたりで編集してたんですが、 同じ会議やジャーナルでもコピペ元が違うと略記の仕方が違ってたりその他色々色々して 全然統一感のない.bibファイルになっちゃってました。

ということで文献管理用のソフトを導入することにしました。 ここ１ヶ月くらい、JabRef を試してみてます。しかしなんだかどうしようもなく重い。あとエラーチェックが甘いというか、 具体的には、他で開いてる最中のPDFをJabRefに"move"（"copy"ではなく）しようとすると、 他で開かれてるのでmoveに失敗するんだけども何もエラー出さずに登録成功したことになって、 あとで開こうとしたときに始めてPDFがないよと怒り出す。10回くらいハマった。

…その他色々、で、だんだん不満がたまってきたので自作することにしました、 というのはまた別のお話として。

他の研究者さん学生さんはどんな感じに文献管理してらっしゃるんでしょう。 オススメのソフト等あれば知りたい。みんな bibtex-mode かな。

最近全然使ってない CiteULike を活用することも考えたのですが、bib 専用というわけでもないので、 ジャーナル名等々をマクロで管理もできないみたいだし、あと、オンラインなので、 見たくなるたびに10MBとかのPDFをダウンロードするのは面倒だなあとか。 PDFを別にローカルに持っておくだけだと、文献リストから一発で飛べないのは ちょっと不便な気がする。CiteULike 自体はソーシャルな機能は非常に素晴らしいのですけども。

16:36 08/02/21

Parsing Techniques

『Parsing Techniques』 ｷﾀ━━━━━━(ﾟ∀ﾟ)━━━━━━ !!!!!

やっと手元に届いたよわくわく。第２版で追加されたというトピックが "generalized deterministic parsers, non-canonical parsers, linear-time substring parsing, parsing as intersection, and parallel parsing" と、どれ一つとってもまったく知らないテーマなので とても楽しみです。

しつこく Project Euler

予想通り面白くなってきました。 今朝解いた 152 すごい楽しかった。数論的な発想だけでは足りず、アルゴリズム的な発想だけでも足りず、 両者合わせてはじめて高速な（手元の Python 実装で 0.1 秒もかからない）解にたどりつくというバランスが絶妙。 正解すると見られるようになるネタバレスレッドでも、一発目の投稿から "This is easily the most beautiful problem of Project Euler I've seen!" と書いてあって、まったくその通りだと思いました。

11:54 08/02/20

Project Euler

やっと Top100 まで来た！

こう、一気にfunnythingさん追い抜かしてやるぜ！と威勢良く言ってみたいところなんですが、 正直、残り全問目を通してみても、ぱっと見で解けるのが一問もなくなってしまいました。 逆に言うとここからが面白いところですね。 ちなみに、ここまでで苦戦したのは 44 と 78 でした。でしたっていうか 78 はまだ解けてないです。O(n^2) 時間で計算できる範囲に 解が見あたらなかったのでどうしたものかと…。

ドラクエ３

百万ゴールドの男 が いよいよ佳境に差し掛かっているのでみんなディスプレイに穴が空くほど読むといいよ！ バラモス戦とか凄い好きだ。

17:53 08/02/18

内包表記

list comprehension の話 … と直接関係はないのですが、他の言語のはともかく、Python のは結構改善できるとこがあるように感じるんですよね。 まず let や val のようなのが無い上に式しか書けないので、 複雑な式を変数に置きたいときに

[v  for line in sys.stdin
    for k, v in [line.split()]  if k in tags]

しょっちゅうこんな謎のループを一個増やしてるんですが、これはなんとかならんのだろうか、という。 いくらなんでも酷いので自分が何か根本的に見落としてるんだと思うんですが。 上手いやり方どなたかご指導下さい。

[v for k,v in (line.split() for line in sys.stdin) if k in tags]

この変形はとっさに出てこないし、要するにブロックのチェインと同形になるので、 JOINへの要求 あるいは 出てくる変数が複数 という奴で、 もっと外側でも line を参照したいときに困る。うーむ。

もう一つが、やっぱり for や if より最終的な値の式を後に置きたいなあ… という希望が。 Ruby のブロックの方がすっきりして見えるのはこれが大きいのではないかと思う。イメージ図：

[for line in sys.stdin
   for k, v = line.split() if k in tags:  v]

Haskell なら do 記法で書けばこう書けるし、Scala にはリファレンス見る限りこっちしか無かったりする？（不明） なぜ後に置きたいかというと、 変数を宣言するより先にその変数を使った式を書くというのは自分にはおよそ不可能な芸当なので。 SQL の SELECT なら "変数" 相当の名前は既に宣言されてるので良いのですが…。

15:56 08/02/16

Project Euler

やっと Top200 まで来た！

だんだん "solved by" と自分が感じる難易度が離れてきて、次どれ解くのが楽かまったくわからなくなってきました。

10:04 08/02/15

BeOS

Haiku の名前。 コードネームで呼ばれるようになった最初の BeOS のバージョンが "Genki" だったりと、 元々、日本語から名前取ってくる文化がどことなくありまして。 "OpenBeOS" から名前を変えるときの投票でもそういう方向になったのでした。 Be に標準添付のブラウザがエラーメッセージを全て 5-7-5 で伝えてくる面白君だったので、 特に "Haiku" は海の向こうの Be な人に印象強かったんじゃないかと。

ちょっと前の記事 に関連するけど、 自分が初めて自分から出した英語メールがこの名前決める流れの時だったので記憶に残ってます。 「誰か日本語知ってるヤツ、"Beauty"の意味の日本語って何？」 「"Bi" だよ。発音 "Be" とほとんど一緒だからいいんじゃね？」 「でも "BiOS" って BIOS かよ」 みたいなやりとり。ほんとどうでもいいな。

メタマス！

ちょっと前の記事に関連すると言えば、 Kolmogorov-Chaitin complexity がいかに楽しそうな話であるのか、 池上さんが メタマス！の紹介 を通して語っておられます。みんなこれ読んでうっかり楽しそうだなと思って Kolmogorov-Chaitin complexity について知りたくなって勉強して私に説明してくれるべきである！

Chaitin の著書は『数学の限界』 しか読んだことがなくて、他も気になってるんだよなー読まないと。

18:43 08/02/14

遅延評価よりも IO が難しい

たまに研究方面の話でも書いてみる。なお、タイトルは釣りです。

call-by-value （≒正格評価）と call-by-name （≒遅延評価）という言葉は ご存じな方が多いような気がします。

function f(x,y,z) { return x+y }

f( factorial(3), fibobacci(4), ackermann(5,6) ) → f(6, 3, なんか巨大な値) → 6+3 → 9     // cbv
f( factorial(3), fibobacci(4), ackermann(5,6) ) → factorial(3) + fibonacci(4) → 6+3 → 9 // cbn

関数を呼ぶときに、先に引数を全部評価してから関数の中身に移るのが call-by-value で、 逆に、先に関数の中に入ってから、実際に引数が使われるタイミングで引数が評価されるのが call-by-name。 call-by-need については今回は考えない。なかったことにする。

二者の違いですが、まあ、大差ありません。 上の例のように call-by-value だと実際は使わない引数まで無駄に計算しちゃったりして時間がかかったり、、 もっと酷いと、cbn なら終わる計算が cbv だと無限ループで止まらなくなったりするかもしれません。 ですが、どっちの戦略を取るにしろ「最終的に計算が止まるなら返ってくる値は同じ（合流性がある）」という意味で、そこまで差はないと言えます。 これがもし違ったりすると、cbv の言語で育った人が Haskell に慣れるのは今よりもずっと大変だと思う。

さて、非決定性計算 が入ってくるとどうなるでしょう。

function foo()  { return 1 or 2 (非決定的に) }
function bar(x) { return x+x }

bar(foo()) を call-by-value で計算すると…

bar( foo() ) → bar(1) → 1+1 → 2
             → bar(2) → 2+2 → 4

答えは、2 か 4 のどっちかです。一方、call-by-name で計算すると…

bar( foo() ) → foo()+foo() → 1+foo() → 1+1 → 2
                                       → 1+2 → 3
                            → 2+foo() → 2+1 → 3
                                       → 2+2 → 4

2 か 3 か 4 が返ってくる可能性があります。つまり、cbv と cbn では計算結果が違ってしまうのだ！

本題

形式言語理論の方面では、call-by-value, call-by-name のことをそれぞれ IO と OI と呼んだりします（関数呼び出しの引数＝括弧の内側＝Insideを先に評価するのがIOで、 外側Outsideを先にやるのがOI、です）。

どっちが良いかというと、どっちにもそれぞれの良さがある、みたいな感じです。 例えば、さっき"非決定性計算"でリンクしたSICPのambでパズルを解く例は IO じゃないとどうしようもない。 (require (not (= fletcher 5))) と (list 'fletcher fletcher) の fletcher が違う値になったりしたら何をやっているのかわかりませんから。 逆に OI は、なんというか説明しづらいんですが、対称性一貫性があって、 理論を OI で考えると綺麗に行くことが多い。プログラムで考えずに文脈自由文法みたいな 文法定義言語の方向で考えるともーちょい具体的にOI凄いっていう例もあるけども略。

で、今ちょっと研究してるテーマは出来れば IO で考えたいものなんですが、 関連する過去の研究はことごとく OI でやってるものばかりなんですよね。 自分で IO の場合に応用しようとしても、確かにこれは OI で証明したくなるわってものばかりで、 どれもIOだと最初の一歩をどっちに踏み出せばいいのかすらよくわからない。 IO 難しいなあ。

19:09 08/02/12

コルモゴロフ複雑性

学科のMLに流れてて知った "Introduction to Kolmogorov complexity and algorithmic randomness" ってめっちゃ聴きたいんですけど！ 誰か聴いてきてまとめてください頼む。

英語バグレポの心構え

Dスレ見ててちょっと考えました。 英語でバグレポート したいんだけど英語苦手！ というあなたに送る。

まず Yukiwiki - バグレポートのための単文集 から引用させてもらいますと、もう、これに尽きます。

バグレポートの目的は何か? バグを伝えることである。よりよい英語を書くのが目的ではない。 拙い英語でもいいから、とにかく書け。 ネイティブスピーカーなら、変な英語でもそれはそれで通じる。 日本語ネイティブは FreeBSD-users-jp:72469 を理解できるっしょ? それと同じ。

実際、自分の英語だって酷いもんです。でも、それで通じたので、まあ今回も通じるだろうと勢いで書いちゃえる。 通じるかもしれないけど下手な英語書くの恥ずかしい…というのはあるかもしれない。けどさ、別に、 外国の人が拙い日本語書いてても「こいつ日本語下手だなﾌﾟﾌﾟ」とか絶対感じないじゃないですか。 むしろ逆な印象を持つと思う。 それと同じで、ネイティブじゃない人が多少アレな英語書いてても誰もなんとも思わないよ。

で終わってもいいんだけど

もうちょっと具体的に考えるか。 「でもどうしても自分の英語の変さを減らしたい」って人はどうしたらよいだろうか。

# 以下は決して、「英語が上手くなりたい」ひと向けの文章ではありません。そんなもの俺が知りたい。

1. コードで語る。 言語処理系やライブラリのバグレポに話を限っちゃいますけど、 「英語が苦手なら英語を書かなければいいじゃない」戦法。 バグを再現する最小限のコードと、それを実行したときの出力と、期待される正しい出力を並べればいい。

nullpo.d:
int main() { printf("NullPo"); return 0; }

> dmd nullpo.d
> nullpo
Ga!

It should be "NullPo".

こんなんで終わっちゃえばいい。あなた自身もプログラマなら、 「どういうバグ再現例を見せられたら一番わかりやすいか」、よくわかっているでしょう。 もちろん、そんな風に単純な例を示せないこともある。そういう時は仕方ないので英語を書こう。 どうやって書くか。

2. 知らない単語を使わない。 知らない構文も言い回しも使わない。 個人的には、これが変じゃない英語を目指すための最重要ポイントではないかと思ってます。 「日本語だと○○○なんだけど英語でなんていうのかわからない」、そんなときは辞書を引くはず。 でもそこで自分の知らない単語が出てきたら、その単語は使ってはいけない。

例えば "変な結果になります" って言いたくなったときに ALC で "変な" を引くと、1番目に "birdie"、2番目に "bizarre" などと出てきます。 こんな単語、意味わかります？わからないよね？わからなかったら使っちゃダメです。 次を見よう。3番目に出てくるのが "comical"。これは馴染みのある単語かな。 馴染みのある単語だから、ここで comical を使ったら意味が違っちゃうことがわかります。 コミカルな結果って、なんか違う。

辞書で出てきたからって無条件で意味を知らない単語を使ってしまうと、知らず知らずのうちに、 コミカルな英語になってしまうかもしれません。知ってる単語で、意味があってることを確かめて使えば、 比較的安全。"変な" の例でいうと、辞書で見つかった残りのうち funny と odd と strange は、 私にとっては知ってる単語でした。なので、この辺を使って英文を書き進めます。

知らない単語を除いたら何も残らなかった！ そんな時は、日本語の方を言い換える。 例えば、"変な結果になります" を、"結果がおかしいです" に言い換えて、"おかしい" で辞書を引いてみたり。 日本語なら皆さんプロでしょうから、5通り10通りの言い換えは常に可能なんじゃないかと思います。 そうやって言い換えては辞書を引き…を繰り返してると、そのうち、知ってる単語がでてきます。

単語に限らず知らない文法や言い回しも同じことで、決まり文句 や複雑な文法を使わなくても、言いたいことは言えます。少なくとも、日本語なら言えるはず。 そういうシンプルな日本語に言い換えてから英文を考えるといいかも。

3. ググれ。 それでも自分の知ってる単語だけじゃ書けない、ということもあります。 "変な" くらいならいいですけど、もっとマニアックな単語だと本当に知らない語句にしか翻訳できないこともある。 そういうときは、とりあえずその単語でググる。んで、 実際の用例を見て自分の言いたい意味とあってるかどうか確かめる。 あ、その前に、検索にヒットした件数を見るといい。"5件" とかだと避けた方がいい。 あと、やたら日本人のページばっかり引っかかる場合も、それは典型的な日本人英語かもしれない。 なお、単語の使われ方をググるには、 ワイルドカード検索 が凄く便利です。

あと細かいとこ。 三単現の -s のつけ忘れ/つけ過ぎは非常に多いミスだと思うんですが、実際自分も物凄い頻度でやらかしますが、 これを正しくするのは中学１年生でもできますよね。（主語を単数にすべきか複数にすべきか、可算名詞か 不可算名詞か、などなどは難しいです。でも、動詞の -s を主語に合わせるだけなら難しくない。） 投稿する直前にここ見直すだけでもだいぶ違う気がします。お前が言うなって言われそうですが、まあ。

まとめ

• そんな細かいポイントはどうでもいい変な英語でもそれはそれで通じる

16:34 08/02/11

DFA/NFA

Tclの正規表現の実装 via あちこち を読んでて。Thompsonの方法でNFAを決定的に動かしてるんだったら $0 でも $1 でも $2 でも O(n) で 取れるだろうに何故 O(n^3) なんてことになっちゃってるんでしょうか。よくわからなかった。 Russ Cox 氏自身、昔この解説記事で効率を犠牲にせずにsubmatch情報まで計算できることに触れておられるので、用語の認識にも違いはないと 思うんだけども。backreference なしの例で説明してるのはあくまで例で、このアルゴリズムは backreference ありの場合にも適用できる…ならわかるんですが、そもそも最初に DFA を走らせる時点で backref ありだと無理だよね。うーん。Tcl のソース読むか…。

などと思いながら

暇つぶしにNFAでの線形時間マッチを実装してたら /a|(a)/ =~ "a" で $1 = nil にするのがめんどくなった辺りで 飽きた。→途中の産物

流し読んだ

backref の部分を対応する括弧の中身で置き換えた正規表現でDFA作って近似してから、 上記のアルゴリズムの複雑バージョンを適用してる感じ？ふぉー。

18:14 08/02/07

はるだもん

Fedoraの話などで "HAL Daemon" っていう文字列を見かけるたびに "春でぇむん" が頭をよぎる仲間はきっと大量にいるに違いない！ と思ってググっても全然いなかった、というのが今日の主なニュースです。

Project Euler

ranhaさんに教えてもらった Project Euler を順番に解いてってます。 ふと気づくと熱中しててヤバいですね。例によってとりあえず Python + Psyco で挑戦。 整数演算は十分なんですが、文字列の permutation 全生成を適当に再帰で書いたら C++ での速度感覚に 比べて遅くてちょっと戸惑い気味。list にして std::next_permutation みたいにやるべきかな…。

17:41 08/02/05

MATHEMATIKA'08

MATHEMATIKA'08 また12時まで粘って 7/10 問解けたので満足して帰ったら3問増えてた。

数論っぽい問題の答えを紙と鉛筆でもプログラムでもなんでもいいから解いて送れ、っていうコンテスト。 計算機を"計算"機として使ってる感はなかなか楽しいな。

まだ解けてないの(抜粋)

ログインしないと問題見れないのか…

5x^2 + 14x + 1 が平方数になる自然数 x を小さい順に30個どうぞ

小さい方から順に x=2 (→49), x=5 (→196), ... と。わからなかったのでバカみたいにxに1から順に 自然数入れて平方数になるか試すコードをPsycoさん頑張れーとPythonで回して他の問題解いてたんですが、 21番目までしか見つからなかった…。ペース的にたぶん30番目は10^15くらいの値っぽい。 ちょっとバカサーチは無理だ。ペル方程式のちょっとした変形？とか色々難しく考えてもみたんだけど、 もっとスマートに行けそうな気もする。

1,2,3,4,...,999999,1000000 から 5 個取って、 「四角形の四辺とどっちか片方の対角線の長さ」になってるようにできる組み合わせの個数は？

三角不等式二つ分。謎。

M[i][j] = gcd(i,j)^3 な 10万×10万 の行列 M の行列式を mod 100003 で求めてね。

途中で増えた問題。元々の問題セットに 105×105 バージョンがあって、 普通に基本変形で行列式計算すれば間に合うので数学も何もあったもんじゃなかったのですが、 これは多分gcd(i,j)なことを使うんだよね。どうするんだろう。

20:31 08/02/04

D といえば

Descent 0.5 released。ちゅーことで、D言語のIDEというかEclipse Pluginの最新版がリリースされたそうです。 目玉は "Full autocompletion" ということで、ドット押したらメンバを補完してくれるとか、 クラス名打ち込んだらimportを勝手に挿入してくれるとかそういうあれですが、つまり、こういうことだ。

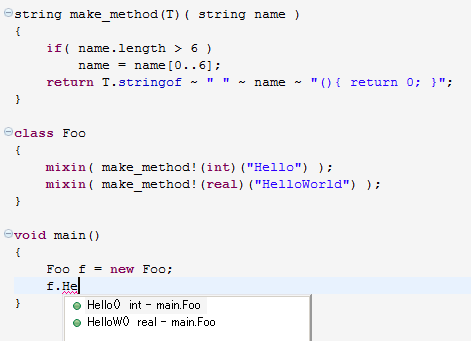
アホだろwwwwじゃなくて、いやはや、頑張るなあ。 D はかなり激しく定数を畳み込むことが仕様に明記されていて、あと、mixin(文字列定数) で 文字列をコードとしてその場に埋め込むことができるので、上のコードで Foo のメンバを補完するには make_method 関数をIDE内で実行しないといけないわけです。

そもそも、コード中にある識別子を全部並べるだけじゃない、context-sensitive な"普通の"補完を してくれるD用IDEすらこれまで自分は知らなかったんですけど（そういう意味で完成したIDEはまだないと書いた）、 一足飛びに凄いことになっちゃいました。 rebuild.exe が最新の DMD に対応してないので実はまだこのバージョンでビルドとか実行とかは試せてないんですが、 これは本気で使えるかも。凄い！

09:55 08/02/04

D言語BOF

BOF ってなんの略だろう…と思って調べて Bug or Feature とか見つけて笑ってたのは秘密だ。 これか。

D言語BOFを
オープンソースカンファレンス2008 Tokyo/Spring　http://www.ospn.jp/osc2008-spring/
セミナー会場にて開きます。

日程：3月1日(土) を希望していますが未定です。
会場：日本電子専門学校 7号館（東京都新宿区・JR大久保駅徒歩2分）
ustreamか何かで中継する予定です。

http://pc11.2ch.net/test/read.cgi/tech/1195394435/659n

だそうです。まだ日時そこで取れるかどうか確定ではないので注意、とのこと。

さて、どっちも遠隔参加だしー、などと気軽にスピーカ参加表明しちゃった結果、 午後だと手元でRPythonでHaskell作りながらDについて話すというカオスな感じになる予感が。

16:35 08/02/01

Pluggable Type Systems

あろはさんとこのコメント欄で、 XMLの「ボヘミアンと貴族」 の話題が出てたのを見て思い出しました。 これに当たる議論がプログラミング言語の世界にもあって、 すなわち "Pluggable Type Systems" なのではないだろーか、という。

これは Gilad Bracha 氏（invokedynamic の中の人であり Strongtalk (型付き高速Smalltalk) の中の人である） が提唱している考え方で、@IT の記事にあるボヘミアンの主張を改変コピペすると……

• 「静的型は構文上の制約でしかなく、プログラムに意味を与えるものではない。 同一のプログラムに対して、異なる型を使っても、複数の型を使っても、型なしで使用しても問題ない。」
• 「プログラムは、静的型がなくても、動的に処理を行うことで実行することができる。」

……言語の意味論は、型システムは、そのように設計されているべき、という主張だと思います （ボヘミアンがスキーマ不要論者でないのと同様、これも決して、静的型不要論ではないので注意）。 私は正直言うとスライドと論文ナナメ読んで、あぁこれ面白そう重要そうだなーと呟いてるだけの レベルなので、どなたかきっちりまとめてみると面白いと思うんだ！

P! H! P!

Re: PHPのマニュアルで一言。 基本的に、各関数のリファレンスと一段上のページを合わせて見ると やっと情報が完全になるように書かれているような感じがします。＞PHPのマニュアル

• preg_*
  • デリミタとしては、英数字およびバックスラッシュ(\) 以外のすべての文字を使用可能です
  • パターン構文 のとこにメタ文字一覧があります
• ereg_*
  • 使える表現は POSIX 1003.2 を見ろとの記述があります
  • んで、そこに all other special characters, including `\', lose their special significance within a bracket expression.
  • [[:<:]] と [[:>:]] は、BUGS (略) The syntax for word boundaries is incredibly ugly. なんて記述が残ってるところから見ると、混乱してるのは POSIX ERE の方のような

mbregex については…無いですねえ。