17:53 14/12/22
ソートの逆流れ
クイックソートってあるじゃないですか、クイックソート。
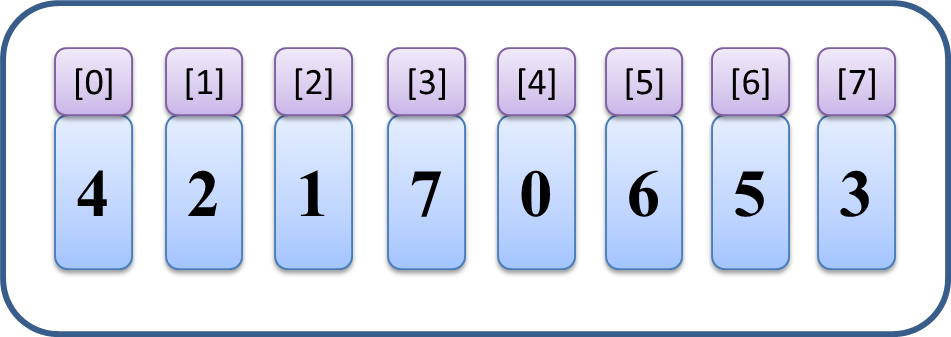
配列、たとえば [4,2,1,7,0,6,5,3] があったときに、
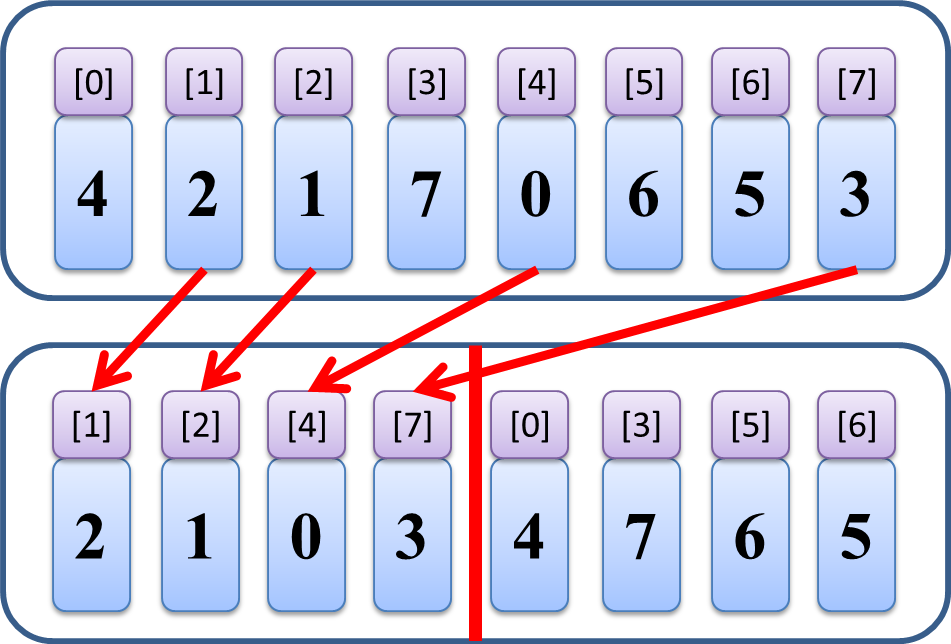
小さい方を左に、大きい方を右にまず適当に集める。
この「小さい方」と「大きい方」への二分割を、いわゆる再帰的に、
分かれたブロック両方で同じ事を繰り返していくと…
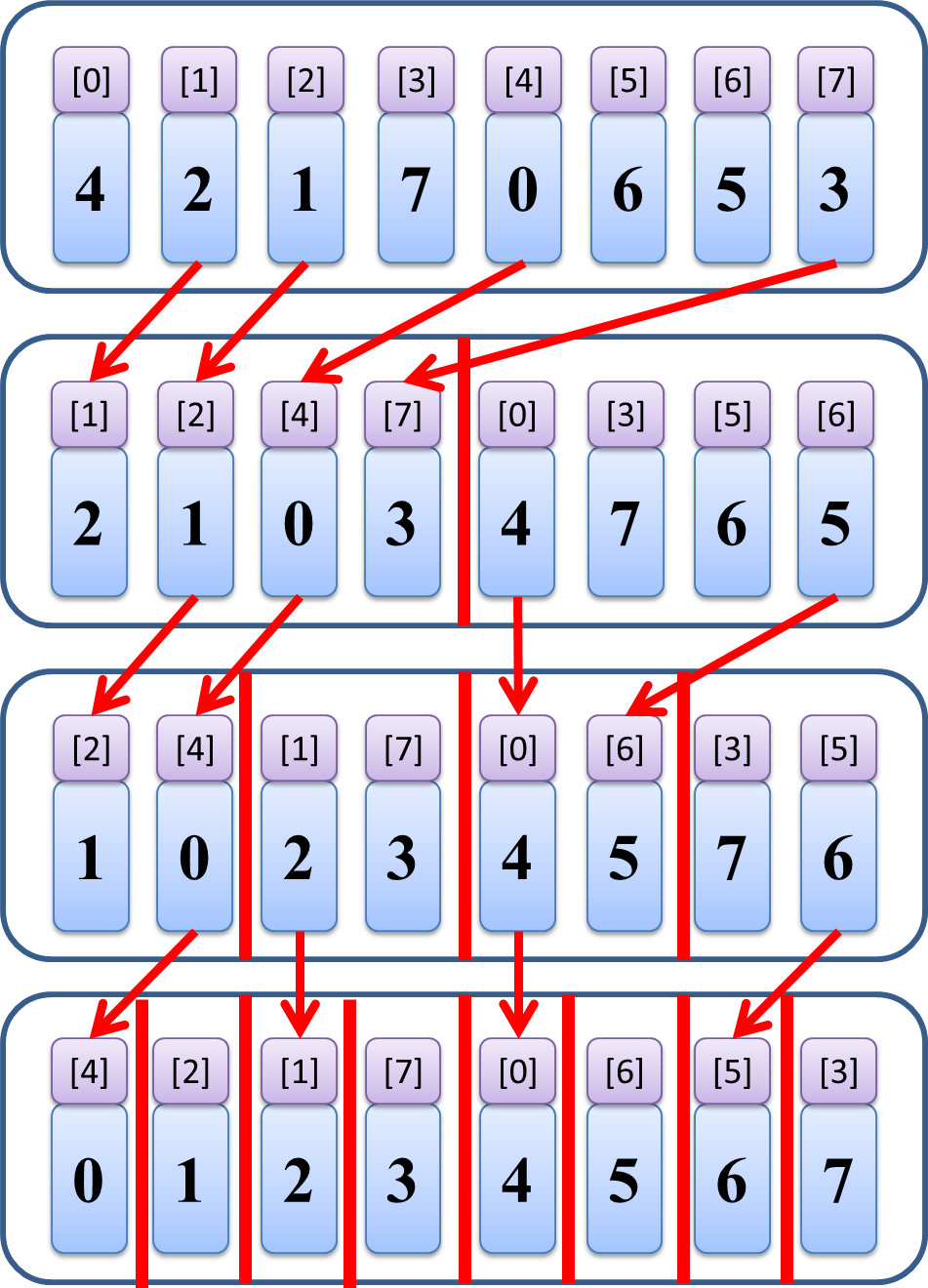
なんと、小さい順に並んだ配列 [0,1,2,3,4,5,6,7] が出来上がるというアルゴリズムです。
逆向き!
このデータの流れを「逆向きに」見てみたい。つまり、ソートが終わった最終状態から話が始まります。
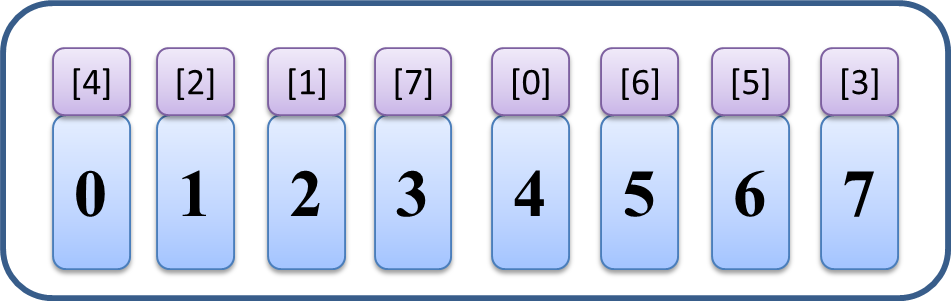
しかも、さっきから説明なしで意味ありげにくっついていた、
「入力配列で元々どの位置にあったか」を表す値に注目していきます。
0の上に[4]がくっついているのは、最初は値0は配列のインデックス[4]の位置にあった、
ということを意味しています。(上のソートの普通の流れ図を確認してそうなっていることを確かめてみてください。)
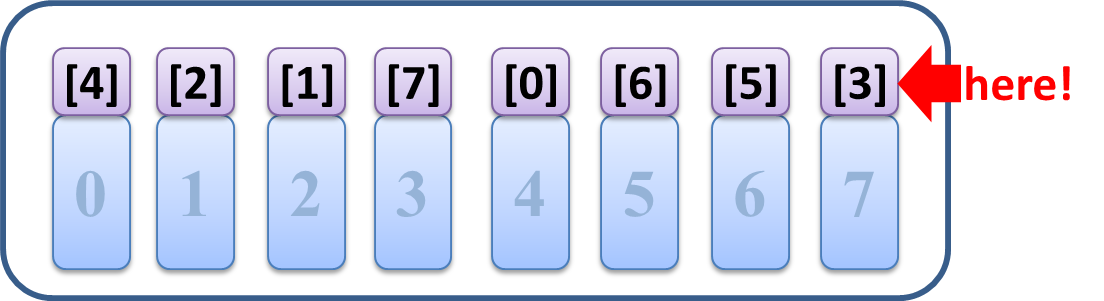
ここに注目した上で、クイックソートの最終ステップ、
サイズ2のブロックを大小に分ける部分を「逆向きに」見ますと…
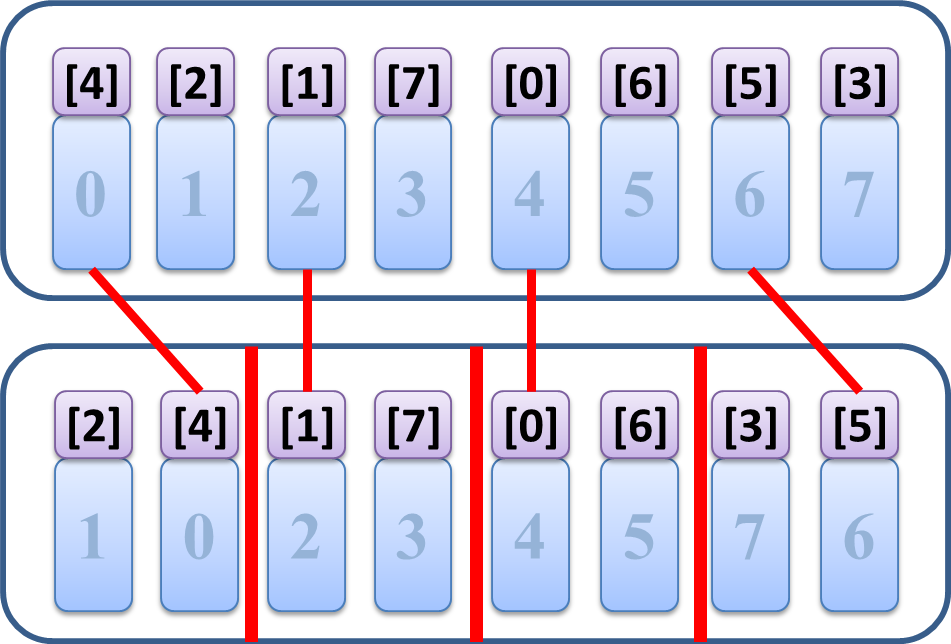
何が起こっているかおわかりでしょうか。上の数字に着目をすると、[4][2] を [2][4] にしたり
[5][3] を [3][5] にしたり、各サイズ2のブロックを小さい順に並び替えていることがわかります。
次のステップを見てもこの通り
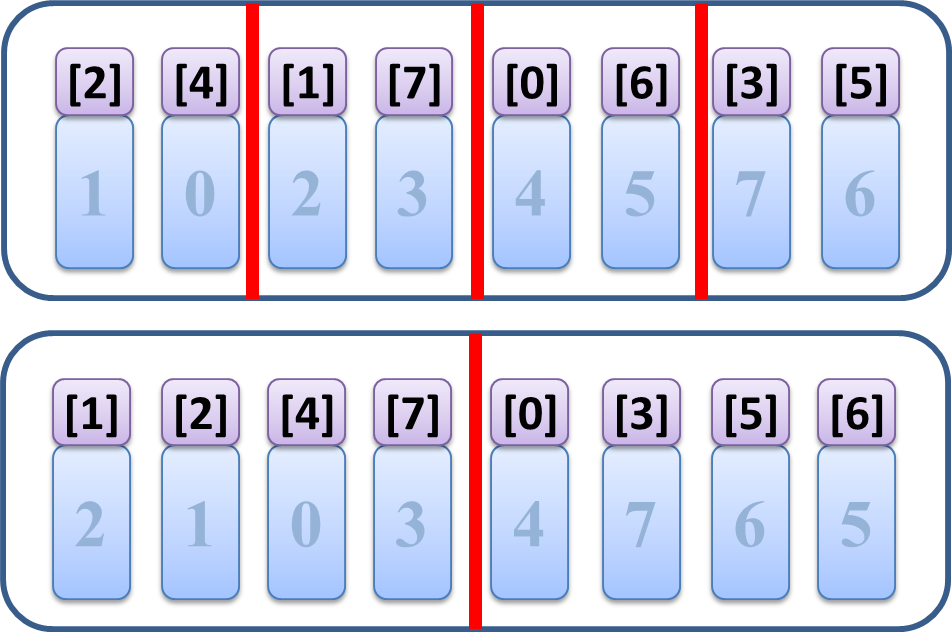
左では [2][4] と [1][7] という二つのソート済みブロックをまとめて [1][2][4][7]
という一個の大きなソート済みブロックを作ったり、
右では [0][6] と [3][5] を集めて [0][3][5][6] にしたり、
小さなソート済み列をマージして大きなソート済み列にする動きが発生していることがわかります。
つまりこれはマージソートの動きですね。
すなわち、こうです。
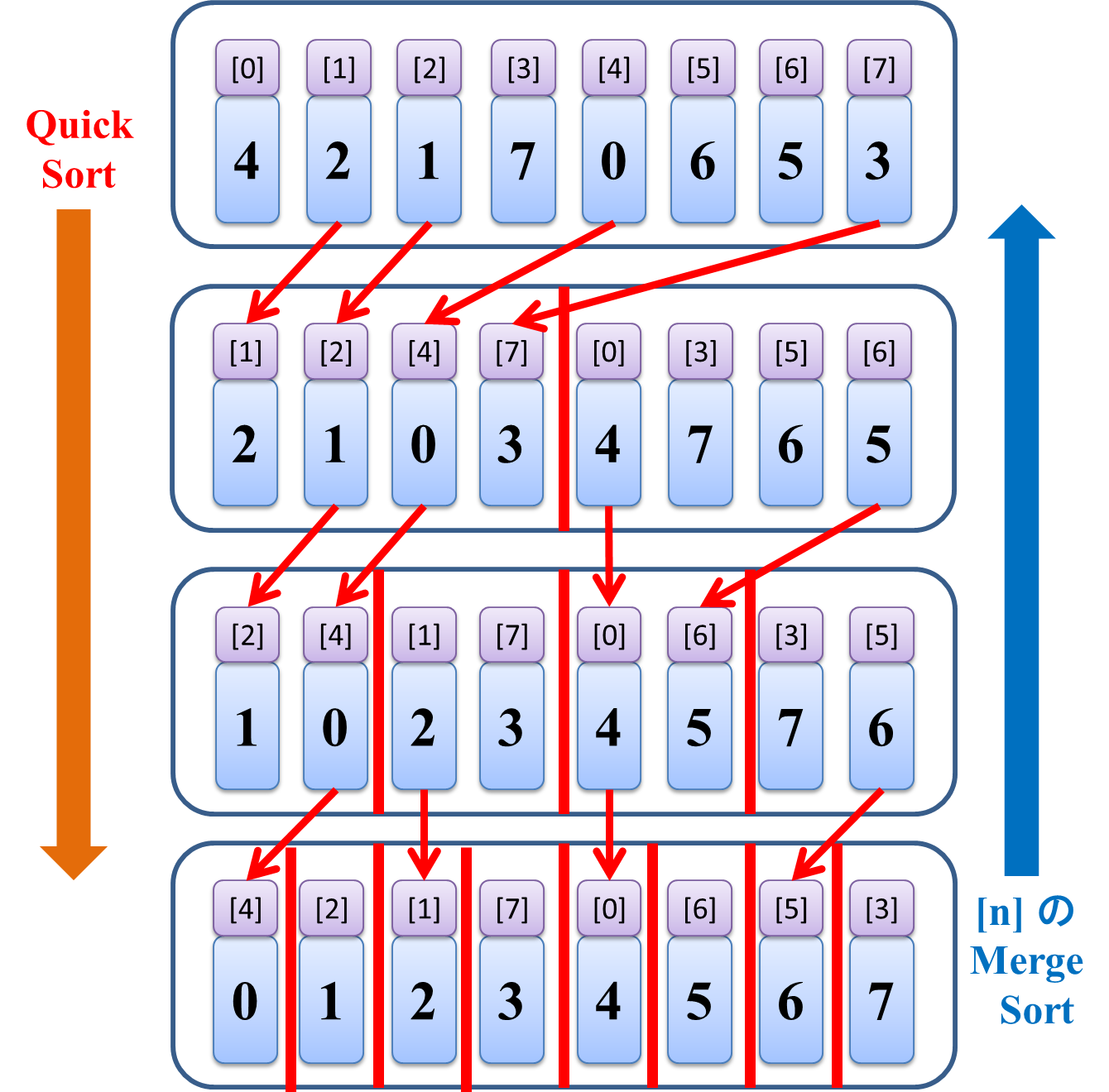
値に関するクイックソートの流れを逆向きから眺めてみると、
[元々値が存在した位置] を基準にマージソートした動きになっていることがわかりました。
データの流れを逆に見ると [元々値が存在した位置] に並び替える操作になっているのは確かなので、
なんらかのソートアルゴリズムになっているのは、まあ、当然と言えば当然です。
が、よく知ったアルゴリズムを逆から見るとまた別のよく知ったアルゴリズムになるのは面白いなあと思いました。
ネタ元
https://twitter.com/kinaba/status/295755050729480193 で、クイックソートとマージソートって感覚的にすごく「似てる」と思うのだけど、
具体的に何がどう「似てる」のか、 数学的にきっちり定式化するとどうなるんだろう??
といった辺りを考えていたら @iwiwi さんが素敵なコメントを一つ下さったのでした。
おもしろいのでまとめておこうと思ったら1年と11ヶ月が過ぎておりました。
ランダムな雑感
・最大値を選んで右に持って行くのを繰り返す「選択ソート」と、
左側をソート済みに保っておいて右から一つずつ正しい位置に値を挿入していく「挿入ソート」の間にも、
同じ関係が成り立っているようです。
挿入ソートを逆から見ていくと、
「元々再右端にあった(=インデックスが最大だった)値を右端に戻す」という操作を繰り返すことになっているので、
これは選択ソートっぽい。
・Prolog などの双方向性があるプログラミング言語で、こういう考え方をダイレクトに実装できるだろうか?
二引数を取る述語で、第一引数だけ決めるとクイックソートして第二引数に出力し、
逆に第二を固定するとマージソートして第一引数を計算するようなの。
・ヒープソート(最大値をO(log n)で管理できるヒープにまずは左から順に値を突っ込んでいって、
そこから順番に取り出して右から順にソート結果を埋めていく)は、逆から見ると
「左から順に値をデータ構造に突っ込んでいって、元のインデックス順に取り出して右から埋めていく」
になるので自分自身と似た構造に戻るのだけど、
途中の構造は元インデックスに関するヒープになっているわけではないのでちょっと違う。
途中のヒープって元インデックス (というかつまり挿入順序)
に関しても何か情報を保っているデータ構造になってたりしただろうか?
(とするとそれを使った違うソートアルゴリズムを作れるか?)
・シェルソートの逆なども、現実に実装はしにくそうなアルゴリズムになっていて、
例えば適当に「345, ..., 7, 3, 1」個おきに挿入ソートするようなシェルソートだと、
逆の最後のステップの直前は、
完全にソートはされてないけど位置を345で割った余りでみるとソート後と同じところまで来ている、
という状態で、そういう状態を軽く作り出せる気があんまりしない。
・そもそも最初のクイックソートもピボット選択など考えずにちょうど真っ二つに分けられる前提で話をしていて、
世の中そううまくはいかないですよね。何かこの「ソートを逆から眺めて見た図」が綺麗に使える場面ってないかなあ。
00:00 14/12/11
[KMP77] を読んでみた
Competitive Programming Advent Calendar 2014 第11日目参加記事です。
文字列の中から指定のパターン(部分文字列)を検索するアルゴリズムの1つに、
考案者の頭文字を取って KMP法 と呼ばれている手法があります。
このアドベントカレンダーの初日でも
『文字列の頭良い感じの線形アルゴリズムたち』
という記事で snuke さんが解説してましたね。
(snuke さんのは検索に一切触れないストイックな解説でしたが。)
このアルゴリズム、色々な教科書や解説サイトで詳しく説明されているので、
自分はそれらの資料だけ読んで把握していました。ところが、
ふと急に思い立って元々このアルゴリズムが発表された際の論文を読んでみると、
KMP法そのもの以上に、論文中で紹介されている問題が面白かった。
ということで、今日はこの元論文の紹介です。
Knuth, Morris, and Pratt. "Fast Pattern Matching in Strings"
SIAM Journal on Computing vol.6, 1977, pp.323-350
第1章~第5章は普通に文字列を検索しています。問題は14ページから始まる第6章。
KMP法を応用すればこんなこともできる!という事例紹介で、突如こんな問題を解き始めます。
一見、検索とは関係がなさそうですが…さて。
長さ n の文字列が与えられる。
この文字列が、偶数長の回文を1個以上結合することで作れるかどうか、判定せよ。O(n) 時間で。
- "xyyx" は長さ4回文そのものなので、Yes。
- "helloollehworlddlrow" は "helloolleh" と "worlddlrow" という二つの長さ10回文の結合なので、Yes。
- "abracadabra" は、どう分解しても偶数長回文の結合にはなってないので、No。
- "abbababbabaabb" は、 "abba" + "babbab" + "aa" + "bb" なので、Yes。
「偶数長の回文かどうか」なら簡単に O(n) 時間で判定できます。
しかし、この問題は、「元の文字列をうまく偶数長回文に分解できるか?」という問題。
分解を全部試すDPなどでは O(n3) かかります。実際これは難しくて、続く第7章では、
"70年にCookの論文で証明された定理の帰結としてこの問題はO(n)で解けるはずなのだが、
具体的な解き方がさっぱりわからなかった" と著者の一人のKnuthが書いていて、
これを解くために本気出して考えたところKMP法に辿り着いたそうです。
自力で解いてみたい方は、ここでページを閉じて考えてみて下さい。
答え(の概要)
というわけで、以下、解答編です。
以下では、回文と言ったらすべて偶数長回文のことを指します。
また、論文にならって、偶数長回文の結合で作れる文字列のことを palstar と呼びます。
(回文/palindromeの正規表現的な意味での*/starにマッチする文字列、という意味だと思います。)
まず、重要な性質として、以下の定理より、分割のやり方は何でもよいことが示せます。
定理: 文字列 s も st も palstar ならば、t も palstar。
全体がpalstarならば、左から適当に回文を削っていっても残りが必ずpalstarになっているので、
巧い正解の分割を探すとか頑張らなくてもよいわけです。証明はこの補題
補題: 文字列 s も st も回文で、s の真の接頭辞で回文なものが存在しないならば、
t は palstar。
を使うと「素因数分解の一意性」みたいなこと…つまりある palstar
を回文の列に完全に分解し尽くすやり方は一通り、
が成り立つので、それを考えるとまあできます。
補題の証明:
s が t より短いもしくは同じ長さの場合は、
st が回文ということはつまり t は s で終わる
(正確には s を逆順に書いたもので終わるんですけど、s も回文なのでこれは s)。
つまり st = sxs みたいな形をしている。
すると x は回文の真ん中なので x も回文だから、t = xs というのはつまり確かに回文の結合で書けている。
s が t より長い場合は、t を逆順にしたものを tR とすると、
逆に s = tRx みたいな形をしているので s = tRxt が回文。
さっきと同じ議論で x は回文なわけですが、s の接尾辞である x が回文ということは、s は回文なので、
s の接頭辞もやはり回文。これは定理の仮定に反するのであり得ない。QED.
というわけで、文字列を左からじわじわ見ていって、
偶数長回文になっていたら即座に確定して最後まで行けるか判定すればよいわけですね。
bool is_palstar(const std::string& s)
{
size_t dekita = 0;
for(size_t i=2; i<=s.size(); i+=2)
if(s.substr(dekita, i-dekita) が回文)
dekita = i;
return dekita == s.size();
}
問題は、素直に毎回回文判定をやると、全体ではまだ O(n2) かかってしまうこと。
工夫が必要です。こうです。
int find_palindrome_prefix(const std::string& s)
{
// s の、偶数長回文になってるprefixを適当に一つ O(|s|) 時間で見つけて返す。
// なければ -1
}
bool is_palstar(const std::string& s)
{
size_t dekita = 0;
while(dekita < s.size())
for(size_t len=2;; len*=2) {
int pallen = find_palindrom_prefix(s.substr(dekita, len));
if(pallen == -1) {
if(dekita+len >= s.size())
return false;
} else {
dekita += pallen;
break;
}
}
return true;
}
長さ2、長さ4、長さ6、長さ8、…と線形に回文を探していくのではなく、
2、4、8、16、…と倍々で探すのがコツで、
長さ k の回文が見つかるまでにせいぜい2+4+...+2k≦4kと線形時間しかかからないので、
トータルでもO(n)行けます。
しかしながら、まだサブルーチン find_palindrome_prefix が残っていますね。
回文判定なら O(|s|) で簡単に実装できますが、
このルーチンがやらなきゃいけない「回文になっている prefix を見つけ出す」処理は、
いったいどうやって実装すればよいのでしょうか?ここでやっとKMP法が登場します。
int find_palindrome_prefix(const std::string& s)
{
s を逆転した文字列 sR からパターン s を見つける文字列検索をKMP法で実行する
}
このように。もし sR の中に s が見つかればそれは sR == s つまり
s は回文ということなので、return s.size() すればよいです。
そうでなくても、KMP法は、
詳細はWikipediaなどを見て欲しいのですが、
走っている途中では「今文字列中で見ている位置はパターン s の何文字目に当たるのか」
を管理するアルゴリズムなので、走りきった最終状態を見ると
「文字列 sR の最後 k 文字がパターン s の最初 k 文字と一致するような最大の k」
がわかるようになっています。
「文字列 sR の最後 k 文字」は「文字列 s の最初 k 文字」R なので、
これはつまり s の先頭 k 文字が回文になっていることを検出できています。
これだけだと奇数長回文が最初に見つかってしまうことがありますが、
最終状態からさらに次の一文字のマッチが失敗したとき辿る表(WikipediaでのT[])を辿ると、
「最大のk」だけでなく、上記の条件を満たす k を全て列挙できます。
というわけで、偶数長になるまで失敗リンクをたどれば偶数回文接頭辞が見つかります。めでたしめでたし。
まとめ
というわけで、自分が今年一番面白いと思った問題の紹介でした。
問題の内容はシンプルながら、
「分割の取り方は任意という数学的考察」
「探索区間を倍々に増やすことで線形時間を保証」
「自分自身の逆転文字列を自分自身で検索」
という、どれ一つとっても巧妙だなあというトリックの3段重ね、見事だと思います。
今ではどんな教科書にもわかりやすく噛み砕かれて載っているような手法も、
たまに振り返ってオリジナルの論文で読んでみると、意外と思いもよらぬ発見があるものですね。








