00:00 13/12/17
シミュレーション問題について
競プロ Advent Calendar Div2013 第17日目の記事です。
シミュレーション問題について書きます。
☆
ところで話は変わりますが、チェスの話をしましょう。
チェスは日本の将棋と違って取った駒を使えないので、ゲームが進むにつれて駒が減っていき、
よく、キング (八方向に動ける、取られたら負けな駒)
とポーン (前方に一歩ずつしか進めない最弱の駒) しか残ってない状態になります。
ポーンは相手陣の一番の奥の列まで進むとクイーンという最強の駒に進化することができるので、
この段階になると、勝負は、
「キングを巧く操ってポーンを守り最奥まで引率して勝つ vs それを阻止して引き分けに持ち込む」
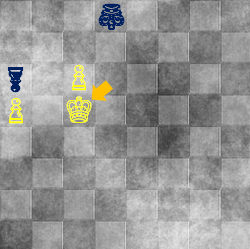
というものになります。以下は有名な局面です。
⇒ 
(チェスは盤面を描くときに駒を上下逆さにしたりしないと思うんですが慣れてない人向けに逆にしてみた。
余計わかりにくかったらすみません。)
黒がピンチです。ポーンの動きは実はちょっとややこしくて、
「まっすぐ前に相手がいなければ前に進める、斜め前に相手がいれば相手の駒をとって斜めに進める」
というものなので、左端の列のポーン達はお見合いして一歩も進めなくなっています。
なので、動けるポーンは白側だけ。黒のキングはこのポーンの残り2歩を阻んで引き分けにできるでしょうか?

さきほどの盤面での最善手は、図の、隣にひとつずれる動きです。
これに対して白が構わずポーンを進めてきたら、元の位置に戻ってポーンをブロックし、
自分の動く場所がなくなることで
ステイルメイト ルールによる引き分けに持ち込めます。
実は、これ以外の手では全て簡単に黒の負けが決まります。
白キングが図のマス (d6) に来たら黒は d8 に行かないといけない、これは絶対手です。
⇒  ⇒
⇒ 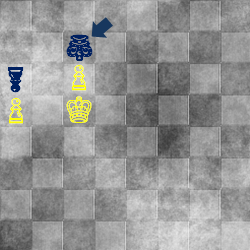
同様に、白キングが c5 に来たら黒は c7 に行かないといけない ことも、数手読むとわかります。
さて、ここからが本番です。白キングが、ポーンの右ナナメ後ろ、d5 に動いたら?
⇒ 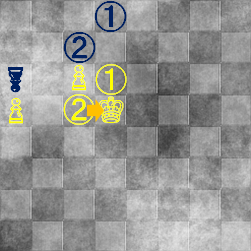
黒はこう考えないといけません。「この次に、白は①に行くことも②に行くこともできる。
自分は相手が白①に行ったら黒①に、白②に行ったら黒②に対応して動かないといけない。
つまり、次に黒①にも黒②にも行ける、両方に隣合うポジションを確保しなければ。」
というわけで正解はここです。
⇒ 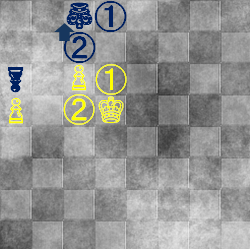
(もう一カ所①②に隣接しているマスは、ポーンの「斜め前」なのでそこに行くと取られてしまいます。)
こうやって絶対手から逆算して、相手の可能な動きをすべて シミュレート
できるポジションを取り続ければ、
無限にポーンを足止めし続け、引き分けとすることができるでしょう…さて、できるでしょうか?
⇒ 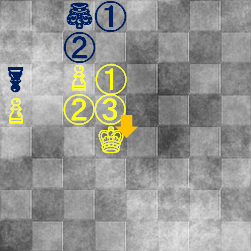 ⇒
⇒ 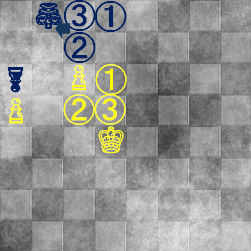
白キングが一歩後ろに下がりました。先ほどと同じ理論で、
「②と③の両方に行く移動をシミュレートできる」場所を陣取らないといけません。
黒①のマスに戻るか、図のように反対に横にずれるかです。そして次の一手。
⇒ 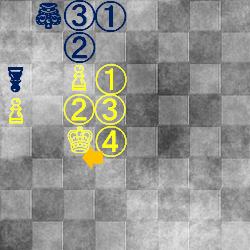 !!
!!
この横移動が決定打です。白が依然として「②と③の両方に行ける」ポジションにいるので、
黒もそれに対応する位置を押さえなければいけません。
が、ポーンの斜め前に行くと取られてしまいます。
一回パスして動かないということができればよいのですが、これはルールです。
キングは必ず8方向のどこかに動かないといけません。
動くと、「次に②と③のどちらかには行けないマス」に移動してしまうので、白に、
その行けない方のマスに動かれて負けます。
というわけで、最初の局面は黒の必敗であることがわかりました。
この、最後にでてきた
「②/③ → ②/③のどちらにも行けるマス → ②/③のどちらにも行けるマス → ②/③」
のような三角形の移動は Triangulation
と呼ばれていて、チェスの終盤戦の基礎技術のひとつです。
☆
ここまでのお話を競技プログラミングっぽくまとめてみます。
これはグラフです。
黒狐のシエルさんと白兎のハナコさんがゲームをしています。
グラフの上を交互に一歩ずつ歩くゲームです。
ハナコさんが1の頂点に来た次のターンにシエルさんは1'の頂点を踏まないと負けです。
ハナコさんが2の頂点に来た次のターンにシエルさんは2'の頂点を踏まないと負けです。
このゲームを無限に続けられればシエルさんの勝ちです。
双方最善を尽くしたとき、勝つのはどっち?
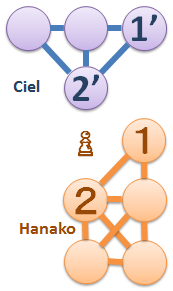
シエルさんの部分グラフにハナコさんのが同型なら自明にシエルさんの勝ちですが、
部分同型でなくても、
たとえば次のようなグラフならシエルさんのグラフの方がむしろ小さいですけども、
無限にハナコさんの動きを追い続けることができます。
つまり、これはグラフの同型問題とはちょっと違った問題になっています。
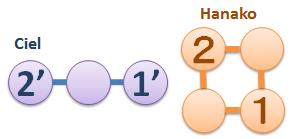
こういう風に、相手と"同じ"では必ずしもないけれど、
重要な観測可能なポイント(頂点1や2)だけは押さえるように、
グラフの上で相手の動きを無限にシミュレートし続けることができるか?
という関係を、(チェスのではなくコンピュータサイエンスの)専門用語で、その名もズバリ
Simulation
と呼びます。
☆
実際に出題された問題で見てみましょう。
といってもアドベントカレンダーの他の日の寄稿者の皆様のようにたくさん問題を解いていないので、
あまり具体例を知りません。むしろどなたか知っていたら私に教えて下さい。
あなたは沢山の部屋が通路でつながった迷路にいます。
迷路の地図も持っているのですが、自分がどの部屋にいるかわかりません。
どの部屋もよく似ていて、つながっている通路の本数くらいでしか区別がつきません。
ウロウロ歩き回ってみれば多少は可能性を絞れるかもしれませんが、
どれだけ歩き回ってもどこにいるか確定できないこともあります。
各部屋について「その部屋と絶対に区別できない」部屋の数を求めて下さい。
SRM 378 Div1 Hard TwistyPassages
問題にするときは、一方が一方をシミュレートできるだけでなく、
双方どう動いても相手をお互いにシミュレートできる関係 (※注) にあるので
グラフの上をうろうろ動いて観測しているだけでは区別ができない
という関係を表す Bisimulation
が問われることが多いようです。この問題もそれです。
とりあえず準備部分のコード。
class TwistyPassages {
typedef int Vert;
typedef vector<vector<Vert>> Graph;
typedef set<set<Vert>> Groups;
public:
vector<int> similarRooms(vector<string> maze) {
// 元の迷路のグラフを入力から読み取る
Graph org = parse_graph(maze);
// 拡大グラフを作る。e2o は拡大グラフの頂点から元グラフへのマップ
map<Vert,Vert> e2o;
Graph exg = construct_extended_graph(org, &e2o);
// 拡大グラフの頂点を"区別できない"どうしのグループに分類
Groups groups = grouping(exg);
// e2oで元のグラフに引き戻す。similar[ov] := 元のグラフでovと区別できない頂点集合
vector<set<Vert>> similar(maze.size());
for(auto& e_grp: groups) {
set<Vert> o_grp;
for(Vert ev: e_grp) o_grp.insert(e2o[ev]);
for(Vert ov: o_grp) similar[ov].insert(o_grp.begin(), o_grp.end());
}
// similar[ov]-1 が答え(グループに自分自身も入ってるので -1 する)
vector<int> result(maze.size());
transform(similar.begin(), similar.end(), result.begin(),
[](const set<Vert>& g){return g.size()-1;});
return result;
}
private:
Graph parse_graph(const vector<string>& maze) {
// 元の迷路のグラフを入力から読み取る。やるだけ。
Graph g;
for(auto& m: maze) {
stringstream sin(m);
g.emplace_back(istream_iterator<int>(sin), istream_iterator<int>());
}
return g;
}
Graph construct_extended_graph(const Graph& org, map<Vert,Vert>* e2o) {
// 拡大グラフの頂点 ev = (v,vi) は、「部屋 v に通路 vi から入ってきた」という状態
map<pair<Vert,int>, Vert> o2e;
Vert ev = 0;
for(Vert v=0; v<org.size(); ++v)
// max(1, ...) は通路のない部屋のための特殊処理
for(int vi=0; vi<max<int>(1, org[v].size()); ++vi) {
(*e2o)[ev] = v;
o2e[make_pair(v,vi)] = ev++;
}
Graph exg(o2e.size());
for(Vert v=0; v<org.size(); ++v)
for(int vi=0; vi<org[v].size(); ++vi) {
// (v,vi): 部屋vに通路viから入ってきた
for(int k=0; k<org[v].size(); ++k) {
// viから見て時計回りにk番目の通路たどると(u,ui)に行く
Vert u = org[v][(vi+k) % org[v].size()];
int ui = find(org[u].begin(), org[u].end(), v) - org[u].begin();
// (v,vi)--k-->(u,ui) という辺を拡大グラフで引く
exg[o2e[make_pair(v,vi)]].push_back(o2e[make_pair(u,ui)]);
}
}
return exg;
}
何をやっているかというとですね、部屋と部屋は通路の本数同じだと区別はつかないけれど、
その部屋に自分がどの通路から入ってきたかとか、そこから数えて何本目の通路かとかは区別できる設定だそうなので、
「部屋×どっから来たか」を状態の単位として使うことにしました。つまりこんな感じに拡大グラフを作っています。
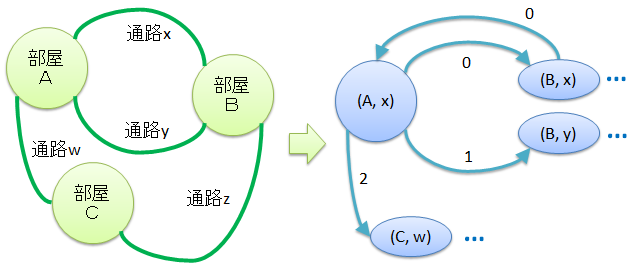
(「部屋Aに通路xから来た状態」から時計回りに0番目の通路つまりxを進むと(B,x)に着く、
時計回りに1番目の通路つまりyを進むと(B,y)に着く、…という感じにグラフを作るでござるの図)
で、本題は grouping 関数、この拡大グラフ上で区別がつかない(Bisimulation関係にある)
頂点はどれとどれか、を計算をする関数です。こんな感じ。
O(E log V) 時間なはずですが適当に書いたのでいささか自信がないです。具体的にはsetのコピーしすぎかもしれない。
// Bisimulation関係にある頂点ごとにグループにまとめる。
Groups grouping(const Graph& G)
{
// 辺を逆向きに参照したいので表を作っておく
// 「reverse_edge[u][e] に v が含まれる」 iff v--e-->u
const int MaxEdgeNum = G.size();
vector<vector<vector<Vert>>> reverse_edge(G.size(), vector<vector<Vert>>(MaxEdgeNum));
for(Vert v=0; v<G.size(); ++v)
for(int e=0; e<G[v].size(); ++e)
reverse_edge[G[v][e]][e].push_back(v);
// まず最初に、即座に区別できるとわかってる頂点を別グループに分ける。
// 具体的には、出てる辺の本数が違ったら区別できるので G[v].size() で分ける。
vector<int> group_id(G.size());
map<int, set<Vert>> groups;
int fresh_group_id = 0;
for(Vert v=0; v<G.size(); ++v) {
groups[G[v].size()].insert(v);
group_id[v] = G[v].size();
fresh_group_id = max(fresh_group_id, group_id[v]+1);
}
// あとは、
// 「現時点では同じグループに入っているけど、一歩進むと違うグループに進んでしまう」
// ような頂点ペアを別のグループにわける作業を変化がなくなるまでひたすら繰り返す。
queue<set<Vert>> partitioner;
for(auto& kv: groups)
partitioner.push(kv.second);
while(!partitioner.empty()) {
set<Vert> P = partitioner.front();
partitioner.pop();
for(int e=0; e<MaxEdgeNum; ++e) {
// gep[gid] := 「グループgidのうち、時計回りにe番目の通路で進むとグループPに入る」頂点の集合
map<int, set<Vert>> gep;
for(Vert v: P)
for(Vert u: reverse_edge[v][e])
gep[group_id[u]].insert(u);
for(auto& kv: gep) {
const int gid = kv.first;
const set<Vert>& enterP = kv.second;
// groups[gid].size と gep[gid].size が違う!
// つまりこのグループの中でも gep[gid] とそれ以外は辺 e で進めば分離できる。
if(groups[gid].size() != enterP.size()) {
// というわけで新しいグループを追加。元のグループは小さくする
for(Vert u: enterP) {
group_id[u] = fresh_group_id;
groups[gid].erase(u);
}
groups[fresh_group_id++] = enterP;
// 新しくできたグループをpartitionerキューに追加。
// 「一歩進むとこのグループに入ったり入らなかったりする」
// という分離をあとでテストするためです。
//
// ここで新しくできたグループの小さい方だけ足せばよいのがポイント。
// A∪Bでも分離できずAでも分離できなかったらBでもできないので、両方試す必要なし。
partitioner.push(enterP.size() < groups[gid].size() ? enterP : groups[gid]);
}
}
}
}
// グループを map<int,set<Vert>> で管理してたので set<set<Vert>> に直して返す。
Groups result;
for(auto& kv: groups)
result.insert(kv.second);
return result;
}
以上です。他の問題の例も。
二次元グリッド(ところどころ壁がある)の空きマスにコインを何枚か置きます。
「上」「下」「左」「右」の4つのボタンがあって、押すと全コインがその方向に1つ動きます。
壁があったら動きません。グリッドの外に行くと落ちて消えます。
壁のせいで1マスに複数のコインが重なることもあります。
このボタンを好きな回数好きな順序で押すことで、「一部のコインだけをグリッドの外に落とし一部を残す」
ことができるような初期配置は何通りありますか。mod 109+9 で。
SRM 563 Div1 Hard CoinsGame
上下左右の4方向グラフで、"落っこちる" イベントによって区別できない頂点はどれとどれ?
という Bisimulation を求めれば、あとは組み合わせの数の計算を適当に掛け算すると求まります。
☆
というわけで、シミュレーション問題についてお話ししました。
シミュレーション問題と言われると競技プログラマの人は、
問題に書かれた規則を律儀に実行していった結果を求めて返す系の作業をする問題を思い浮かべると思うのですが、
まあそこはもちろんこの記事のタイトルが釣りです。
今度こういう系統の問題を見たときに、
あ、「シミュレーション(アドベントカレンダーで見た方)」問題だ!
と名前の印象で思い出していただけたら幸いだなーと思っております。
--------------------------------------------------------------------------
※脚注 "双方どう動いても相手をお互いにシミュレートできる関係":
微妙な表現。Bisimulationというのはお互いがお互いをSimulationしているというのよりもさらに強い条件で、
というのは相手のSimulateに使わないような選択肢の少ない行き先が余計に存在してもSimulateはできちゃいますが、
そういう行き止まりのあるなしで区別はできてしまうので、そういうのがあるとBisimulationの関係にはない等々。
というニュアンスを適当にいい加減に書こうとした結果の表現がこれです。
カクリヨの短い歌
天地明察
さすらう者たち
VS!! (3)
無名草子
明日、ボクは死ぬ。キミは生き返る。
寄せの手筋200
黄金の少年、エメラルドの少女
恋愛視角化現象
ゼロからトースターを作ってみた
おかしな二人
パニッシュメント
タソガレ
いとま申して―『童話』の人びと
睦笠神社と神さまじゃない人たち
式の前日
サクラダリセット2
ウィトルーウィウス建築書
閃光少女
充たされざる者






















 ⇒
⇒ 


 ⇒
⇒ 
 !!
!!


