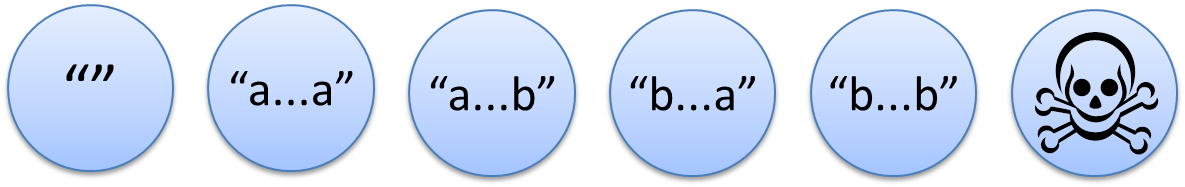d.y.d.

23:21 11/12/22

今年読んだ面白コンピュータサイエンス論文紹介カレンダー第 n (1<n) 週目モードです。

☆ 「難しい問題」
☆ 「名のない関数」
☆ 「演算のせいしつ」

「難しい問題」

[5] R. Impagliazzo and L. A. Levin. "No Better Ways to Generate Hard NP Instances than Picking Uniformly at Random." FOCS 1990.

ランダム生成に興味があります。

パズルゲームを作りました。さて、手強い難易度の面データを無限にランダム生成するにはどうすればいいだろう。プログラミングコンテストの問題を作りました。さて、自動チェック用のテストデータをランダム生成するにはどうすればいいだろう。適当なランダム生成では、簡単なケースばっかり作られてしまい嘘解法に突破されてしまうかもしれません。簡単なケースに偏らない、というかむしろ難しいケースに偏るようなランダムデータ生成の一般論ってないものかな。

ということを呟いていたら @xagawaさんに教えてもらった論文です。以下概要。

... then the P =? NP question becomes academic.

「もし P ≠ NP だとしたら、 NP完全問題は真に "難しい" 問題だということが確定する。例えばハミルトン閉路問題は "難しい" 問題なのだ。」という言い方がなされることがありますが……さて、本当でしょうか？ハミルトン閉路問題の具体例の中でも、簡単なものは簡単です。たとえば極端な話、連結じゃないグラフだったら明らかに巡回できないことがすぐわかる。ちゃんと "難しい" ケースになるように作るのは、それなりの苦労が必要です。

で、その「それなり」ってどれくらい？例えば、十分あり得ることですが、 "難しい"ケースをランダム生成すること自体が"難しい"、つまり計算量が多項式時間を超えるとしたら？その時、たとえ P ≠ NP だとしても、 NP完全問題の難しいインスタンスを作り出すこと自体が人類と計算機にはできない。としたら、理論上はともかく現実にはそれは難しい問題ではないのでは？

というわけで、単に入出力仕様だけが規定された「問題」の難しさではなく、「問題 X と、多項式時間で作れるその入力データ分布 μ の組」の難しさ（平均時間計算量）を、この論文では考えます。 NP問題の中で多項式時間還元を考えたときに "一番難しい" 問題が NP 完全問題ですが、同じような還元によって、多項式時間生成可能分布のNP問題の中で "一番難しい" Samplable 完全問題 が定義されます。さて、このクラスの問題は、はたしてどれほど難しいのか。

結論としては、「工夫いらずでランダムに一様にデータを作れば Samplable 完全になる」 NP 問題が存在するみたい。

「名のない関数」

[5] S. Mirghasemi, J. J. Barton, and C. Petitpierre. "Naming Anonymous Javascript Functions." SPLASH 2011

SPLASH 2011 というプログラミング言語系の会議の期間中であることに気づいて、論文タイトル斜め読みしてたら面白そうだったので読みました。中身はタイトル通りで、「最近の JavaScript ってほとんどの関数が（少なくとも構文上は）無名関数だったりするけど、デバッガのコールスタックに表示する名前が全部 "(anonymous function)" になっちゃうと困るよね」問題。

var zzz = function(){};

の名前を zzz ということにしたり

obj = {hoge: 1, hige: function(){}}

の名前を hige ということにしたり、は結構今のデバッガもやってくれると思いますけど、

var x = (function(){ return function(){} })()

array.each(function(e){ ... })

それをもっと頑張ってみませんか、というような提案をしている論文です。実際この論文の提案する手法や、その結果つけてくれる名前自体は、まあ、ぶっちゃけ「そんなもんか…」という感想を持ってしまったのですが、この問題自体に対して、「こうすればよくなるんじゃないか？」等々自分でも色々アイデアが浮かんできて、色々考えるのが楽しいので印象に残っています。今後しばらくこの手の技術の改善は進むんじゃないでしょうか。

「演算のせいしつ」

[7] S. Rajagopalan and L. J. Schulman. "Verifying Identities." FOCS 1996.

R. E. Tarjan という偉大なコンピュータ科学者がおりまして、彼の名を冠したアルゴリズムが何個あるかわからないくらいなのですが、ある日私が、せっかくなので「Tarjan の論文を古い方から順に読んでって一人盛り上がる会」を開催しようと思い立って読みながら感想を述べるなどしていたら、とても近い内容のお話として @oxy さんに教えてもらいました。

二項演算の仕様が N×N の表で与えられます。例えば bool の AND 演算。

  | 0 1
--+-----
0 | 0 0
1 | 0 1

たとえば {0,1,2} の三値に対する変な演算。

  | 0 1 2
--+-------
0 | 1 0 0
1 | 1 0 2
2 | 2 2 1

crazy演算というものらしい。問題：こういう演算表が結合法則を満たすかどうか判定するプログラムを書け。

結合法則は (x*y)*z =? x*(y*z) という3つの変数に関する等式なので、x,y,zを全通り試せば確認できます。これは N³ 回、演算表を引くアルゴリズムです。さてさて、もっと回数を減らせるでしょうか？ 乱択アルゴリズムを使えば O(N²) でできるよ！という格好いい手法を提案するのがこの論文です。詳しくはスライドにまとめたのでご覧下さい。シンプルな乱択アルゴリズムってどれも面白いですね。

21:45 11/12/15

今年読んだ面白コンピュータサイエンス論文紹介カレンダー第２日の参加記事です。

☆ 「先延ばし屋の予定帳」
☆ 「オートマトンとグリーンの関係の関係」
☆ 「ゲーデル先生の抜き打ちテスト」

の３本を紹介します。論文タイトルは意訳です。

「先延ばし屋の予定帳」

[1] M. A. Bender, R. Clifford, and K. Tsichlas. "Scheduling Algorithms for Procrastinators." Journal of Scheduling 11, 95-104, 2008

1. 序論

今、僕らは、締切の二日前にこの文を書いている。

しかも残念な事に、さっきの文が、論文の中で最初の最初に手をつけた箇所なんだ。締切が明後日ってことは何ヶ月も前からわかってたのに、どうしてこんなになるまで放っておいたんだって？その理由を解明するのが、この論文の目的さ。

というイントロで幕を開ける論文です。ちょっと前に Twitterで流れてきたのを見て興味を持って読みました。なんで面白いと思ったかというと、それはもちろんイントロが面白かったんですが、実は、読み進めていくとイントロどころの騒ぎではなく全体が大変なことになっていました。

内容紹介

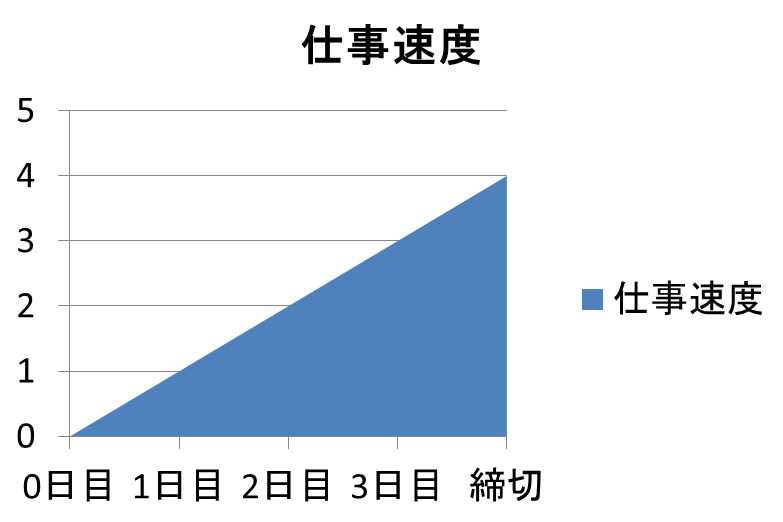
いわゆるジョブスケジューリング問題、「締め切りの設定された複数の仕事があるときに、どの順番で仕事を片付けて行くのが最適か」という問題に関して考察した論文です。ただし、普通のスケジューリング問題では一人の人間や一人のマシンが仕事を処理できる速度は一定であると考えますが、この論文では、 締切が遠いうちはノロノロで全然仕事が進まない、締切ギリギリになってヤバくなると処理速度が上がる というモデルを考えます。まるで私のことのようです。

数学的に言うと、新しく仕事が積まれた時間を r 、その締切を d 、現在時刻を t としたとき、その仕事をこなすスピードは f(t) = t-r、経過時間に比例して上がるものとします。つまり最初はやる気ゼロで、締め切りが近づけば近づくほどグングンと。

さて、やらなきゃいけない仕事が複数あるときに、どれから先に片付けるかの戦略の違いによって、仕事にかかる総時間が変わったり、場合によっては締め切りが守れるか否かが変わってきます。まず論文では、理想的な「最適オフライン戦略」について考えます。これは、「全てのジョブがいつ来ていつ締切か、最初っからすべてわかっている」という状況での最適なスケジュールをを考えるものです。今回の問題設定の場合、締切間際の方がパワフルとわかっているので、すべての仕事は間に合うギリギリまでスタートを遅らせて全部滑り込みで片付ける、と、最短の時間で仕事が済んで幸せです。

さて、これは現実にはありえない理想の最適ケースです。実際には、「オンライン戦略」、未来を完全に見通すことはできずに、新しい予定が投下されてくるなかでスケジュールを決めていく場合の戦略を考えます。普通は、締め切りは守るように注意しつつもどれだけ最適オフライン戦略に仕事時間を近づけられるか、でオンライン戦略の善し悪しを比較するのが通常なのですが…

定理３：最適オフライン戦略なら締め切りを守れるが、オンラインでは絶対に守れない仕事発火パターンが存在する

次にどのタイミングで緊急の用事が割り込むかわからない時は、締め切りの遠い仕事と近い仕事のどちらをこなすのが最適か、どんなに賢くても予測しきれないケースがあることが証明されてしまいます。

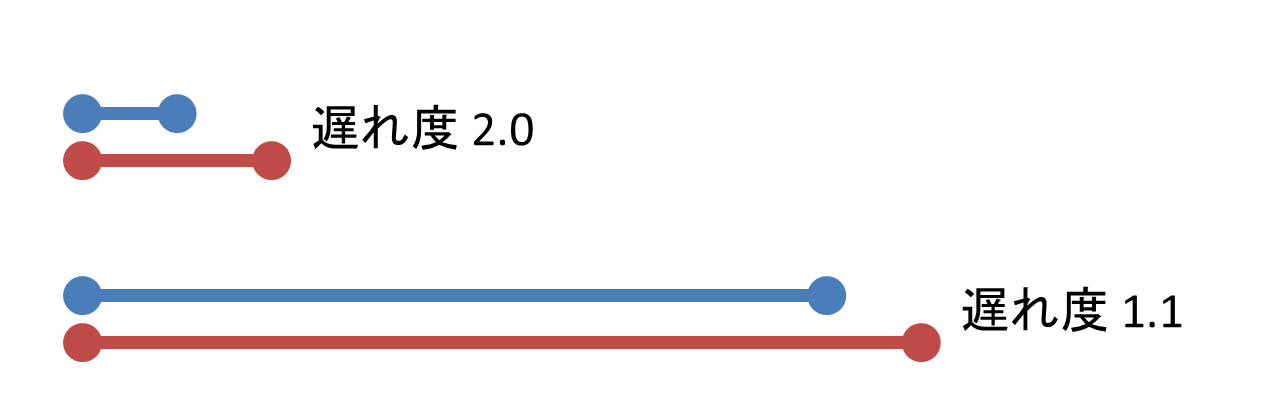
そこでこの論文の著者達は、別の評価基準を導入。ある仕事の開始日時が r 、締切日時が d 、実際に終わらせることができた日時が t （締切に間に合わなかったら t > d になる）だったときに締め切りに遅れちゃった度を (t-r)/(d-r) で定義します。「3日で終わらせてね！」って依頼された仕事に 6 日かかったら遅れ度は 2。でも、「30日で終わらせてね！」っていう仕事に 33 日かかったときは、 30 日に比べたら 3 日の遅れなんて微々たるものだよね！遅れ度はたったの 1.1 です。人間として許されるんでしょうか、この基準は。

というわけで、この遅れ度が評価基準です。あまり遅れすぎない、「遅れちゃった度の最大値を最小にする」戦略が良い戦略とされます。もう締め切りブッチギることが前提になってしまいました。いろんなスケジュール戦略 …… FIFO（最初に来た仕事から順にとりかかって終わらせる）、 EDD（締め切りが近い仕事に優先して取りかかる）、 SRPT（あとちょっとで終わりそうな仕事から順に片付ける）、 LSSF（遅れちゃってる度合が現時点で既に一番ヤバい仕事から順に片付ける） …… などが比較されますが、どれも、最悪ケースを考えると、ジョブの個数 n が増えれば増えるほど最大遅れ度が √n などに比例して増える、スケールしない戦略であることがわかってしまいます。

この問題を解決する THRASHING という最強の戦略を導入して、この論文は終わります。なんと、ジョブがどれだけ来ても、最適オフライン戦略で間に合う範囲なら、 THRASHING なら、たかだか遅れ度 4 しか遅れずに 全てのジョブを片付けることができます！遅れ度 4 というのはつまり、1ヶ月でお願い！と言われた仕事を4ヶ月後に返す感じですね。素晴らしい。

THRASHING 戦略というのがまた凄い。
「仕事の処理スピードは時間に比例する f(t) = t-r と言ったな。だがこの加速が締切で止まるとは言っていない！」

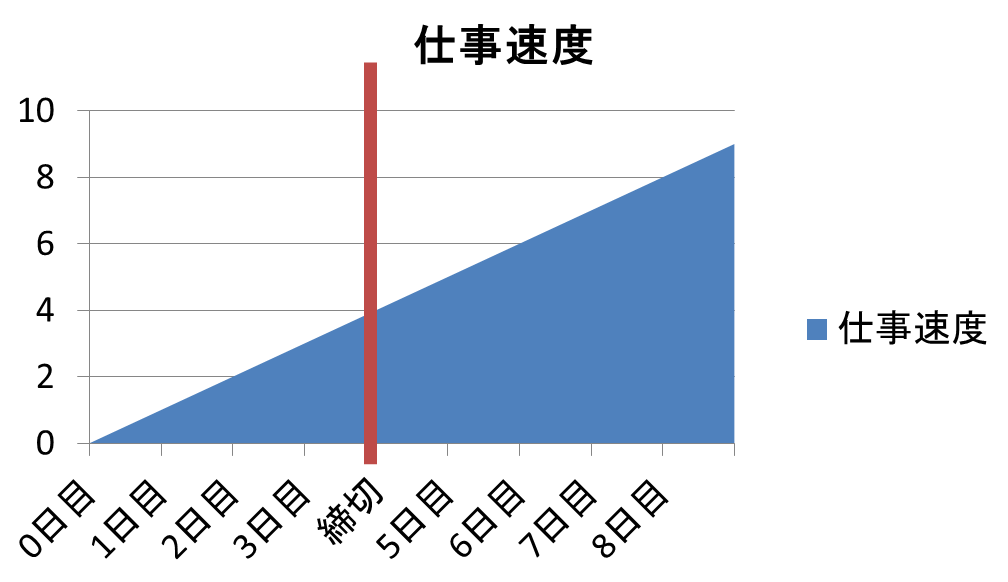
というまさかのお断りのもと、遅れれば遅れるほど無限の力を手に入れることができるので、「遅れ度 2 に達してない仕事には手をつけない。2 に達したもののうち直近で来たタスクから順に片付ける」という、遅刻前提どころか、締め切りを２倍過ぎてないと仕事を始めすらしない、先延ばし屋というレベルでは済まされないメソッド。これが THRASHING で、この戦略をとると４倍遅れることは決してなくて済むそうです。

感想

ちょっとネタ側に倒しすぎた紹介をしてしまいましたが、例えば最後の結論などは「理想のオフライン最適戦略なら 4 倍の余裕がある仕事群であれば、オンライン戦略であっても、全て確実に時間内に仕上げられる」という定理として提示すれば、なにかマトモな感じがしてきます…かな？

…ということを考えるのも野暮かもしれません。そのまま書いてある通りの設定に合致する応用問題が現実世界に転がっているかはわかりませんが、少なくとも、この設定から生み出される純粋に問題そのものは、上で紹介した部分だけでなく、色々と考えさせられるポイントがあって面白い。「もう少し現実的な、火事場の馬鹿力にも限度があるような仕事速度関数にしたら？」ひとつでもすぐに色々バリエーションが生まれてきます。それで十分ではないでしょうか。

ところで第一著者の Bender さんのサイトを見てみると、「常習犯」で、他にも色々オモシロ論文を書いてらっしゃるようです。他に

[2] M. A. Bender, M. F.-Colton, and M. A. Mosteiro. "INSERTION SORT is O(n log n)." Theory of Computing Systems 39, 391-397, 2006

という、衝撃的な出落ちタイトルの論文も楽しかったです。ネタのような導入から、なかなかどうして全く非自明で興味深い問題を引っ張り出す腕は見事だなあと思いました。

　　☆

↓ 以下２つは、面白論文は面白論文でも、爆笑論文系ではなく、ふつうに学術的に興味深い論文の紹介です。 ↓

「オートマトンとグリーンの関係の関係」

[3] T. Colcombet. [PDF] "Green's Relations and Their Use in Automata Theory." LATA 2011

要旨

このサーベイ論文の目的は、モノイドのイデアルの理論、いわゆる Green's Relation を紹介することと、オートマトンにまつわる問題への挑戦の道具としての、その有効性を示すことにある。

一本目のキャッチーなイントロの論文紹介で読者の皆様のハートを（多分）つかんだところで、私の趣味の世界に入ります。 正規表現とオートマトンの話をしましょう。さて、上に引用した部分、ほとんどの方には謎すぎる用語で埋め尽くされていると思いますが、まず、モノイドというのは単に結合法則（＋α）を満たすもののことを、ちょっと気取った呼び方をしてみただけです。文字列の結合演算は結合法則を満たしているモノイドであります。以上。この論文は、数学の、モノイドの理論の眼で、つまり結合法則ラブラブ大好き光線を通して、正規表現というものを理解してみました！というお話になります。

なんでこれを読んだかというと、著者さんの論文いつも面白いので定期的に欠かさずチェックしているからなのです。この論文でも紹介されている Factorization Forest という概念の紹介がとても面白かったのでした。

内容紹介

さて、去年紹介したように、正規言語は文字列の世界を有限通りに分類します。論文では、「a と b だけが並ぶ文字列だが、 "aa" という a の２文字連続は含まない」という正規言語を考えていました。この例は、世界を６つに分けます。

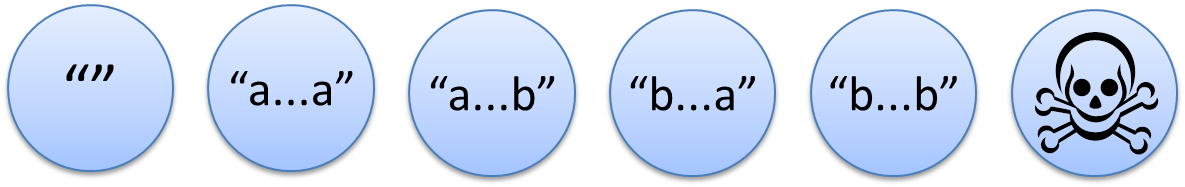
空文字列
aa を含まない、a で始まって a で終わる文字列
aa を含まない、a で始まって b で終わる文字列
aa を含まない、b で始まって a で終わる文字列
aa を含まない、b で始まって b で終わる文字列
aa を含む文字列

「"aa" という a の２文字連続を含まない」というパターンにマッチするかしないか、それだけの基準で見ると、この６分類以上に細かい区別は必要ないのです。 "aba" も、 "abbbbbababba" も、どちらも同じ。なぜなら、どんな文字列 s を持ってきても、前者を後者に置き換え s.replace("aba", "abbbbbababba") あるいはその逆、どちらをしても「a の２文字連続を含まない」かどうかという性質は変えられないから。

こんな風に、単にマッチするしないの二値分類だけではない、正規表現の裏にはもっと細かい分類が隠れているのだ！という見方は、既に一つ、興味深い視点です。でも、もう一歩先に進むこともできます。

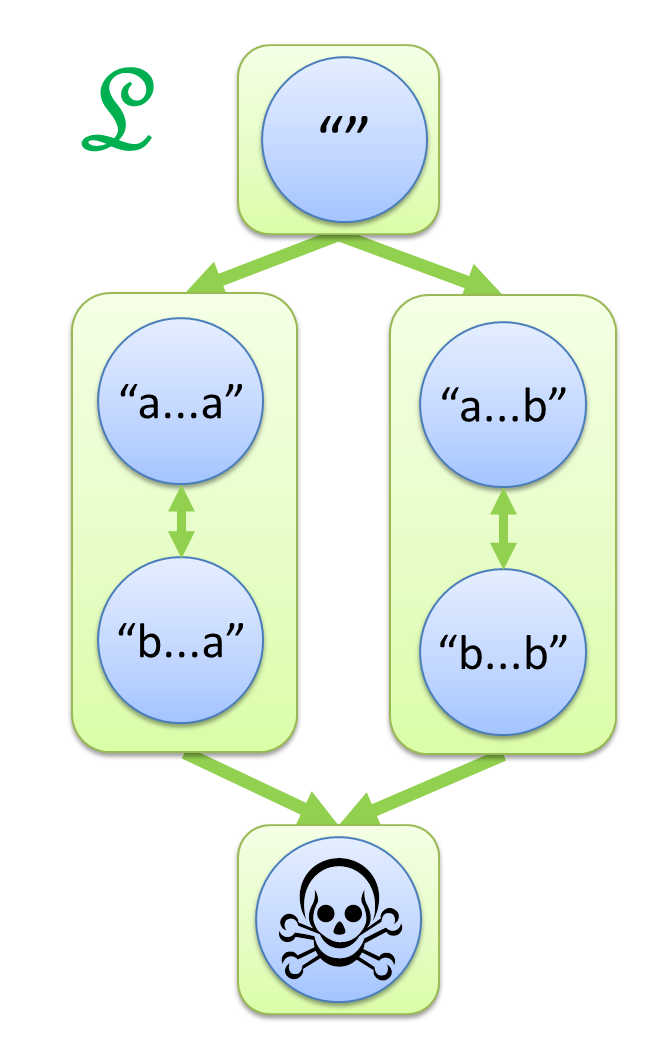
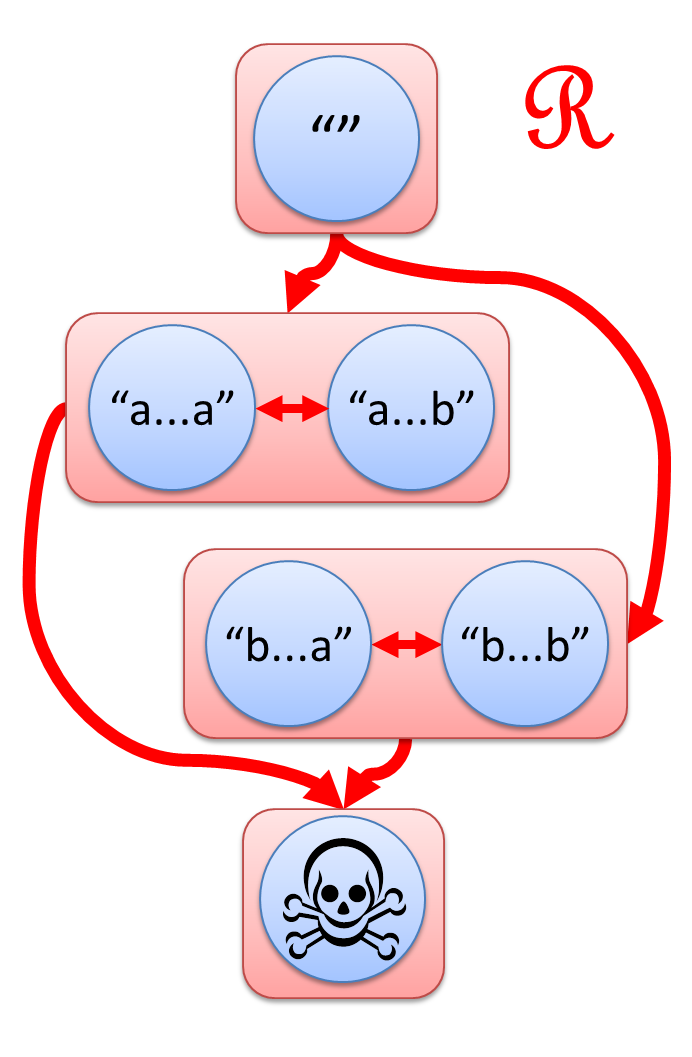
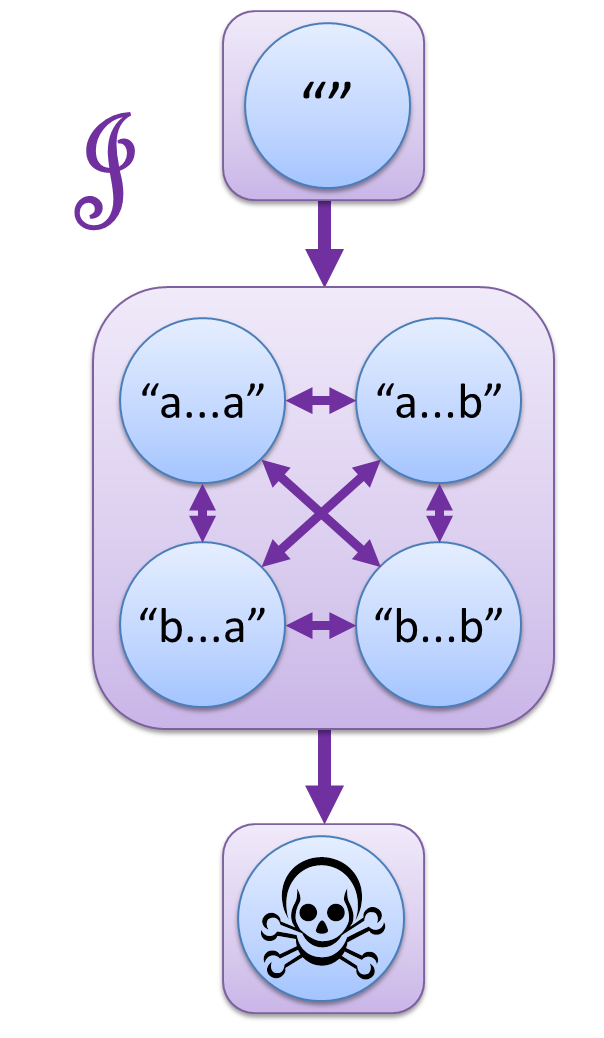
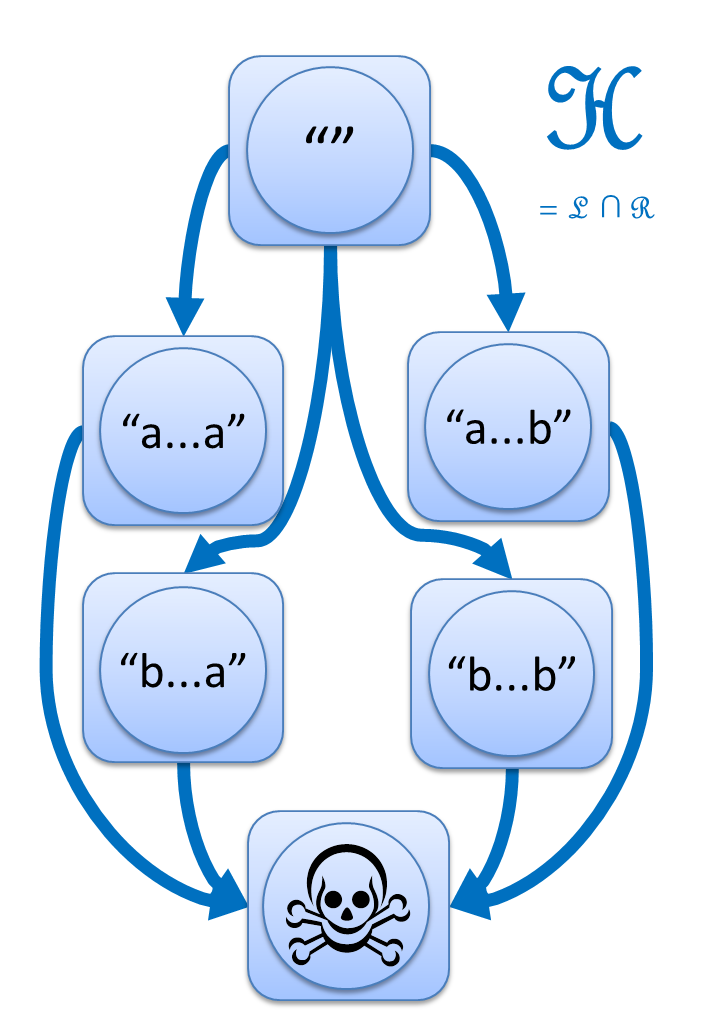
この論文は、６つに分かれた世界の間に、L, R, J, H の４つの矢印を導入するという視点を紹介します。

s ─L→ t とは、s の左に別の文字列をくっつけて t にできること。
s ─R→ t とは、s の右に別の文字列をくっつけて t にできること。
s ─J→ t とは、s の左右両方に別の文字列をくっつけて t にできること。
s ─H→ t とは、s ─L→ t かつ s ─R→ t、つまり左からくっつけても右からのくっつけでも t にできること。

神秘的な図形が浮かび上がってきました。この図こそが、「a の２文字連続を含まない」の真の姿なのです！（※ 上の図では "" から髑髏マークへの矢印は省略しています。）

数学では Green's Relation として知られているものですが、これを、正規表現やオートマトンの世界で知られている４つの定理やその証明などを、この図の上で解釈すると何が起きているのか、どんな意味があるのか解題してくれたのが、今回紹介した論文です。具体的には矢印の表す順序関係の上で帰納法したり、矢印で互いに行き来できる"強連結成分"のサイズを計ったりです。

感想

「今では私も、この視点を道具にバリバリと新しい定理を証明できるようになりました！」 …と言うことができればいいんですが、実際はそんなことはなく、はーなるほどなー面白いなーと既存の証明を眺めるのみです。

とはいえ、ふと正規表現を見たときに、この J, L, R, H の矢印の図を描いてみることはできます。そうやって理解してみる、というのは、知らずに自力で編み出せるようなことは絶対なかったでしょう。そんな、絶対自分一人ではたどり着けなかったなあ、という物の見方を一つ知れたことは楽しいなあ、といったことを思っています。

「ゲーデル先生の抜き打ちテスト」

[4] Shira Kritchman and Ran Raz. "The Surprise Examination Paradox and the Second Incompleteness Theorem." Notices of the American Mathematical Society 57, 1454-1458, 2010.

「来週の月曜日から金曜日までのいずれかの日に抜き打ちテストを行う」
これを聞いたある学生は次のように推論した。（「抜き打ちテスト」という言葉を論理学的に推論しやすくするため、「ある日にテストが行われることが、前日までには予測できないテスト」であると定義する。すると、以下のように推論できる。）

まず、金曜日に抜き打ちテストがあると仮定する。すると、月曜日から木曜日まで抜き打ちテストがないことになるから、木曜日の夜の時点で、翌日（金曜日）が抜き打ちテストの日であると予測できてしまう。これは、先ほどの「抜き打ちテスト」の定義に矛盾する。よって、金曜日には抜き打ちテストを行うことができないということが分かる。

次に、木曜日に抜き打ちテストがあると仮定する。…

- wikipedia:抜き打ちテストのパラドックス

@tri_iro さんのつぶやきを見て面白そうだなーと思ったので読みました。最近は基本的にTwitterドリブン論文読みです。

内容紹介

以下、厳密にちゃんと理解している自信がないのでテクニカルに正しくない記述が残っている可能性がありますが、変なところがあったら基礎論クラスタの人はボコボコにして下さい。

無矛盾かつ十分に強力な公理系には、証明も、否定の証明もできない文が存在する

というのが、かの有名なゲーデルの第一不完全性定理を大ざっぱに述べたものです。第一不完全性定理の証明は、嘘つきのパラドックス、「"この文"は偽である」という文は真としても偽でもおかしい、というパラドックスとの類推で理解されることがあります。すなわち、 「"この文"は証明できない」 という文を、強力な公理系なら書くことができて、これは証明できるとしてもできないとしてもおかしい。

無矛盾かつ十分に強力な公理系では、その公理系自身の無矛盾性を証明できない

第二不完全性定理です。第一不完全性定理の言っている、 "証明も否定もできない文" の意味のある例を１つ与えます。十分に強力な公理系では、上に書いた第一不完全性定理の証明がそのまま実行できるので、仮に自身の無矛盾性を証明できたとしてしまうと、繋げることで「"この文"は証明できない」が証明できてしまう。矛盾。

ところで、証明も否定の証明もできない文の具体例は、これだけではありません。チャイティンという人が、最短プログラムを目指すコードゴルフを使って、そんな例を構成しています。プログラミング言語を一つ固定して、 Golf(n) = "そのプログラムで自然数nを出力する最短プログラムのバイト数" と定義しましょう。「自然数を出力だけってゴルフ問題として簡単すぎない？」と思うかもしれませんが、例えば Golf(1111...(1億個)...1111) は、単純なループで書けるので1億桁のランダムな数を出力するより遙かに易しい。いかにパターンを見抜くかという熾烈な争いになります。円周率1000桁勝負など、実際の名ゴルフ勝負です。

話が逸れました。

十分に強力な言語なら、ある定数 L が存在して、どんな自然数 n に対しても "Golf(n) > L" は証明できない

例えば Ruby には Rubyゴルフ定数 が存在して、たとえばそれが 100 だったとすると「100バイトでは書けない」タイプの命題、「円周率1億桁を100バイト以下のRubyプログラムで出力することはできない」のような命題はすべて絶対に証明できない、と言っています。

このゴルフ定理は、Berryのパラドックス、つまり「１７文字で/定義できな/い最小の自/然数」という言明はその自然数を定義しているじゃないですか！というパラドックスに類推した証明がなされます。十分に強力なプログラミング言語なら定理と証明の全列挙ができるので、『「Lバイトかかることの証明がある自然数」を全探索の末見つけたら返すプログラム』が書けます。このプログラムは、そんな自然数が存在すればその数を出力しますし、 L を定数リテラルとして埋め込めば log L + α バイトで書けるので、 L を十分大きく取れば L より短いです。矛盾。「そんな自然数が存在すれば」という仮定がおかしい。

さて。

このゴルフ定理も証明できない命題の例を示していますから、第一不完全性定理の証明になります。ところが、ゲーデルの嘘つきパラドックスに似た証明と違って、ゴルフによる証明からは、第二不完全性定理がそのまま滑らかに導かれることはありません。

コードゴルフによる証明の延長線上にあるような第二不完全性定理の証明は、ありますか？

それを見つけたのが、この論文です。冒頭に引用した 抜き打ちテストのパラドックス を思い起こさせる技を使うことで、「無矛盾と仮定すると………………ゴルフ定数を考えることで…………矛盾」という形で第二不完全性の証明を完成させます。

抜き打ちテストにおける週の日数にあたるのが、「x ≦ 2^L+1 かつ、（超えることが証明できるかはさておき）Golf(x) が実際 L を超える自然数 x」の個数だそうです。奇妙な推論により、これが 1 個ではないことがわかる → 2個ではないこともわかる → 3個ではないことも… という不思議な推論の連鎖をつなぎ、結論が導かれます。

感想

これも、言われなければそういう考え方を絶対自分はしなかっただろうなあ、と思える考え方を植え付けてくれた、という面白さですね。楽しいです。

おしまい

もっと論文の数で攻める記事にするはずだったんですが、書き始めたら個々の紹介が止まらなくなってしまいました。ノルマの３個でタイムオーバーです。２週目が回ってきたら続くかもしれません。ではでは。お次は @dmikurube さんです。

21:48 11/12/09

未来の証明言語を考える

Theorem Proving Advent Calendar 第９日の参加記事です。マシンにわかるプログラミング言語でプログラマがプログラムを書くがごとく、「マシンにわかる証明記述言語で証明erが証明を書く」という遊びについてのアドベントカレンダーだと思います。よろしくお願いします。

さて最近流行りつつある定理証明と定理証明系に関する Advent Calendar です、とイベントのページには書いてありますが、正直、個人的な感想をぶっちゃけて述べると、今のままの Coq や Agda では、100年たっても流行らないと思います。だって、その、難しすぎますよね。こんなの日常的に書くの、無理でしょう。この前は bool 配列のソートの正しさ一つ証明するのにも一苦労でした。一苦労というか、時間内にできてないですし…。

といって、じゃあ、証明記述言語という概念そのものが100年たっても流行らないかというと、そんなこともないんじゃないか、とは思っています。なんというか、そう、「夜明け前」感を感じるのです。構造化プログラミングもオブジェクト指向も関数指向も契約による設計もテスト駆動もなかった頃のプログラミングは、今よりもずっとずっとずっと、大変だったと思います。それが証明言語の今なのではないでしょうか。そうだ、という根拠は特にあるわけではないですがまあ気にせず、そうであるならば、誰かが新しい証明言語パラダイムを考え出すのを嘴をあけて待っているよりは、自分で切り開いて行きたいものです。

というわけで、ときどき、自作証明記述言語の言語仕様を妄想しています。

妄想だけで何一つ形になっていないので非常にダメダメな上に、どれも何一つ具体性がなく方向だけの感じで、しかも世界で1000人くらい考えている感じで独創性がなくもうダメダメのダメダメですが、今日は、その恥をいくつかさらしてアドベントカレンダーのネタと言うことにしようと思います。自分がメインで使っている証明言語は Coq なので、不満の持ち方も、多分にCoqに囚われています。新しいパラダイムとかそういうレベルでは到底ない雰囲気です。ご了承下さい。

1. 停止性を気にしない。 Coq では、書くプログラムはすべて「無限ループしないでちゃんと計算が終わる」または「ちゃんと（ある意味で）１状態先に進む」物でないといけない、という制限があります。再帰関数を書くたびに、まずはこれを必ず証明しないと先に進めない。これが結構腹が立つところで、冒頭であげたソートの例だと、「まずは結果が必ずソート済み列になっているという性質から証明してみよう」と思っても、関数を書いた時点でいきなり停止性の証明の義務が立ちはだかります。今気になってるこの性質だけ証明したい！と思った時に変なものが邪魔をする感は結構強いですし、そもそもこれのせいで簡単な例題というものが存在しにくくなっている、のは流行らない原因になりうる。といって、停止性証明を黒魔術で全てすっ飛ばすような書き方をすると、 Coq などの証明の正しさ自体が停止性に依拠しているので、他の証明の正しさも全て保証されなくなってしまう。 というわけで、 「停止しないかもしれないけど停止したらこの型 A の値になる」ということを意味する型、 ○A (仮) のような概念を導入して、必要なところだけ A を要求、必要ないところは ○A で、のような依存型のシステムが欲しいなあ、ということを考えていました。そして存在するようです→ "Partial Objects in Type Theory"。これは Nuprl で今も使えるのかな。そして、調べてみると、なかなか巧くはいかないらしい。「停止しなくてもいい」を導入するからにはそのシステムでは無制限な再帰／不動点演算を許したいわけですが、 fix :: (○A→○A) → ○A を無造作に導入すると、型 A によっては、健全でないシステムになってしまうそうな。つまり、「fix で書いたプログラムは止まるかどうかわからないけど止まるなら型Aの値を返す」と型の上では書いてあるのに、止まって、しかも、型Aじゃない値を返してしまうパターンが、 dependent product があると作れてしまうそうです。これを避けて実用的にするのは、大変そう…。

2. Proof Carrying Data？ "Formal Certiﬁcation of a Compiler Back-end" という、「Coq で書かれた正しさの保証されたコンパイラ」に関する論文がありますが、導入として、「正しい」コンパイラの３分類をあげています。一つ目は Certified Compiler、コンパイル関数 compile :: source -> target に対して、定理証明系を使って「どんなソースSについても、欲しい性質 P(S, compile S) が満たされる」という定理を証明してやるというスタイル。これで作ったコンパイラは、以降、どんな入力に対しても「正しく」振る舞うことが保証されます。二つ目は Proof-carrying code、これは、コンパイラは、コンパイル結果を出力すると同時に、「結果が正しい」ことの保証書を同時に出力するというスタイル。"保証書"はもちろん形式的に定義されていて、「ちゃんと適合する保証書がついていればそれは正しい」ことは保証されている。これで作ったコンパイラは、正しいコンパイルをすることも、正しい保証書を出すことすらも、何も証明されていないので、全然変な物を出す可能性はあります。けれど、「でてきたものをチェックしてみて正しかったら本当に正しい」と言うことはできる。三つ目は、論文読んで下さい（省略）。当然、一つ目より二つ目のほうがルーズな感じなんですが、「証明は難しいけど実際問題として正しくは動いている」ようなプログラムの場合、後者で実際は十分なわけです。特にコンパイラの場合、実際に仕事をするのはコンパイルした後なわけで、その時点でそこにできたプログラムの正しさがしっかり保証されていたらそれで十分で、「未来永劫出てくる可能性がある全てのプログラムが正しいことの保証」なんてのは要らんわけです。あと"保証書"という物自体色々便利とか。なんですけど、Coq とかは、Certified Compiler を書く方をアフォードするような言語設計になってる気がするんですよね。というわけで、考え得る全てに対するプログラムの正しさを定理証明する、というスタイルではなくて、データとその保証書のセットを持ち回って後でチェックできるデータを常に作るスタイルの証明支援系言語、コンパイラだけに限らずそういうのがあれば面白いかもしれません。

3. 好き勝手公理系を乱造する指向言語。そもそもですね、またぶっちゃけると、自分、「プログラムの正しさ」とかにあんまり興味がないんですよ。正しさを保証したいんじゃないんです。証明が書きたいんです。 定期的に言ってますけど、プログラムのテストでも、テストで正しさを保証したいというのは半分くらいで、半分は、「テストしやすいようにコードを書こう」と方向付けることで自然と整理された再利用しやすいコードになる、という効果が嬉しいのでそうしています。同じく証明でも、証明しやすいように書こうとすると自然と整理されて意図の明確に分離されたコードが書けるのが嬉しいから、証明が書きたいのです。で、この効果は、「意味論がきっちり定義され健全、無矛盾な公理系に基づいた証明を厳密に書く」のじゃなくても相当程度得られるのではないかなーということを考えています。「この証明とこの証明を組み合わせればこれが証明できる」という、ある程度の基本事実を列挙して俺俺公理系として定義して、それに従ってロジックを組み合わせるのだ、という流れの記述言語の部分さえしっかり存在してれば、コードの構造をマトモにしコードを書きやすくする効果は得られる気がする。謎の論理システムを投げ込むと正しさとかそういうのは意味が無くなってしまいますが、それはそれ、別問題です。

…近年マレに見る脳内をダイレクトに垂れ流すだけの記事になってしまいました。まさかこんなことになってしまうとは。

結局何が言いたかったかというとですね、趣味で自作俺俺最強プログラミング言語を作って妄想言語機能について熱く語る相手は、周りを見渡せば今なら結構見つけられますけど、そういえば、なかなか、趣味で自作最強証明記述言語について語ってる人って見ないですよね、と思ったので、まあみんな語るといいんじゃないかな！ということです。以上！

あ、あと、いつものように「それ○○でできるよ」と「それ△△でダメだしされてるよ」情報はお待ちしています。

00:01 11/12/07

アルゴリズマーのためのゴルフのススメ

Competitive Programming Advent Calendar 第７日の参加記事です。よろしくお願いします。

Code Golf という遊びをご存じでしょうか。普通のゴルフはボールをカップに入れるまでの打球回数の少なさを競いますが、コードゴルフは、問題を解くコードの文字数の少なさを競います。 Short Coding とも言います。詳しくは shinhさんの連載をどうぞ。

コードを短くする工夫の中には、普通使わない言語仕様の隅を突いてみたり、一つの文に全ての計算をごっちゃり詰め込んだり、泥臭い部分もたくさんあります。でも、どれだけ泥臭い技で短くしたとしても、大元の方針、問題を解くアルゴリズム自体が悪ければ、最短コードは生み出せません。最後に勝負を決めるのは、結局 TopCoder や Codeforces と同じ、どれだけ良いアルゴリズムを考えることができたか、だと思っています。

今日はそんなわけで「競技プログラミング好きの皆様ならゴルフもきっと面白いですよ～」という主張を、特にそういう色が強い実際のゴルフコンペの問題を例に繰り広げます。

速いは短い

そうでない場合も多々ありますが、計算量のオーダ的な意味で速いプログラムは、同時に短いことが多いです。

Biggest sum of a coherent subsequence (SPOJ Shortening Codes)

　入力：長さ n (1≦n≦10⁵) の整数配列（-10⁹≦要素≦10⁹）。
　出力：その配列の連続する部分列の総和の最大値を求めてね。

ナイーブに全ての部分列を列挙して総和を計算すると O(n³) 時間、累積和などの工夫で総和の計算を高速化して O(n²) 時間などの解もありますが、 O(n) で解けます。難しくはないですが自明でもない難易度だと思います。 Div1 300点くらいかな？

そして、書いてみるとすぐわかりますが、短いのも O(n) 解です。乱暴な言い方をすると、例えばC言語なら for(;;) という7バイトの文字列を3個も含んでるコードと1個しか無いコードを比べるわけですから、少ない方が短くて当然です。

こんな風にループの少ない、あるいは整理され場合分けの少ない綺麗なアルゴリズムを思いつく力は最短解に直結します。

たった１つの変数で

ゴルフでは、時間/空間計算量以外にも重要なリソースがあります。そしてそのことがたまに、面白い問題を提起します。

Elias delta to Fibonacci (Anarchy Golf) の部分問題

　入力：フィボナッチ数列 1, 1, 2, 3, 5, 8, 13, ... に属する自然数 n （2≦n≦10⁷）。
　出力： n の直前のフィボナッチ数を求めてね。

フィボナッチ数列を作るには、直前の2項を覚えて順に足していったり、 2x2の行列をかけ算していったり、現在のフィボナッチ数そのもの以外の補助的な値も覚えておいて、次の値次の値を生成するのが普通です。

ところが、ゴルフでは、変数の個数というリソースも重要です。変数宣言が必須な言語では、変数を減らせば減らすだけ宣言の分のバイト数が稼げますし、そうでなくても、2つの値を適切な値に更新するには二つの式が必要ですが、もし1つだけで管理できれば、一つの式で済むので短いです。さて、他に補助変数なし、いきなりフィボナッチ数１つだけを与えられて、ダイレクトに直前や直後のフィボナッチ数が求められますか？

当時の私はその方法が時間内に思いつかず、 2変数で下から上るようなコードをやむを得ず書いて

a,b = 1,2
while b!=n: a,b = b,a+b
return a

6バイト差でトップに負けました。悔しい…！トップの人のコードは、 [ネタバレ防止のため透明文字→] (n+1)*2584/4181。フィボナッチの一般項 ((1+√5)/2)ⁿ-((1-√5)/2)ⁿ を考えるとわかりますが、後ろ半分は1より小さい数のn乗で、だいたい無視できるので、必要な精度の黄金比を割ったり掛けたりすれば前後に動けます。 [←ここまで] でした。好きなゴルフ解のひとつです。

プログラム探索

探索するプログラムを書くんじゃなくて、条件を満たすプログラムを探索する、なんて場面も楽しいです。

CODEHASH (TLE'09)

　任意の文字列を、英大文字32文字にハッシュするハッシュ関数（リンク先の問題文参照）があります。
　「この関数で自分自身のソースコードをハッシュした結果を出力する」プログラムを書いてね。

これはC言語のコンテストだったので、自分のソースコードを文字列として読み込むといったことはできませんから、なにか定数文字列を出力するプログラムを書いて、それが偶然自分のハッシュと合う、という状況を狙って作り出すしかありません。

main(){puts("COMPETITIVEPROGRAMADVENTCALENDAR");} // たまたま当たったらいいな

実は、問題のハッシュ関数は簡単な線形関数なので、後ろに変なコメントをくっつけると自由に狙った値にハッシュ値を調整できて、 "JJJJ...JJJ" になるように狙い撃ち、というコードを私は提出しました。

main(n){for(;n++<33;)putchar(74);}//ORNDRVGOKYROOFPKNCQMHIEWMISXDRN

この方法は簡単ですが後ろに32文字近くゴミがつくので、長くなってしまいます。変なゴミを伸ばさずに、出力する文字列を "JJJ" とかじゃなく、巧く選んで自分自身を出したい。といっても、今のハッシュ値に合わせようと出力を変えると今度はハッシュ値の方も変わってしまっていたちごっこです。 26³²通りの全探索すれば偶然一致するものはあるかもしれませんが、そんな全探索は終わりません。賢く候補を絞らなければいけない。アルゴリズムパワーの出番です。この問題は、ハッシュ関数が線形関数であることを考えると、自分自身を出せるという条件は 32元連立合同式の解であることと同値になります。頑張ろう。

コードゴルフに大切なもの

変数の個数だけではありません。いろいろ、普段とはちょっと違う視点でアルゴリズムの善し悪しを評価する機会があります。

Reverse (Code Golf)

　入力：スペース区切りで、1 から n までの数がちょうど一回ずつ出てくる文字列。
　出力：先頭のa₁個をreverse、先頭のa₂個をreverse、…、先頭のa_k個をreverse、としたら入力の配列がソートされる a₁ … a_k を求めてね。

たとえば入力が "2 3 4 5 1 6 7 8 9" なら、先頭4つを反転して次に先頭5つを反転すれば 1 から 9 が順に並ぶので、 "4 5" を出力すれば答えになっています。答えは何通りもあるので、どれを答えてもいいです。最短手順を求めなくてもいいです。

最短でなくてよいので、端から順に合わせていけば簡単です。反転操作をすると先頭側が毎回変換してしまうので、後ろから合わせていくのが楽でしょう。「2手で最大値nを一番後ろに持って行く」「2手でn-1を後ろから2番目に」「以下繰り返し」とする 2n 手の手順は簡単に作れます。

でも、この手法にはひとつ、重大な欠点があります。それは、入力を全部読み込んでからでないと処理が開始できないこと。「入力を配列等に読み込む」というステップと、「配列等から添え字アクセス等で値を取り出す」というステップが分離してバイト数を食う分、入力をバッファにためる解はどうしてもハンデを負います。読み込みと計算を融合できた方が、短い。

言語に依るので一概には言えませんが、この問題で Ruby の場合、挿入ソートの要領で 先頭から順に値を挿入して揃えていく「4手で先頭1個をソート」「4手で先頭2個をソート」「4手で先頭3個をソート」「以下繰り返し」の4n手解に軍配が上がりました。出力するものが多い分長くなるにも関わらず！

全体を見ずにデータを先頭から逐次処理していくタイプのアルゴリズムを オンラインアルゴリズム と言って、応用面でのメリットから様々な研究がされています。オフラインでは分が悪く、綺麗なオンラインアルゴリズムを見つけ出した方が勝ち、という勝負が気軽に日夜行えるのは、現時点ではコードゴルフだけじゃないかと思います。

パラレルパラレル

さっきの reverse 問題ですが、（Rubyで）先頭から入れる解の方が短くなるのには、もう一つ理由があります。擬似コードで比較してみましょう。後ろから解：

a = 入力全体を読み込み
for k = n to 1:
   i = a.index(k) # k の位置を探す
   puts i, k  # こういう風に反転 [hoge k fuga] ==> [k egoh fuga] ==> [aguf hoge k]
   a = a[i+1 .. k].reverse + a[1 .. i-1] # 反転後こうなる

先頭から解（の一例）：

a = []
for k = 1 to n:
   v = 一要素読み込み
   i = (a&[0..v]).size # !! aの中でvより小さいものの個数 !!
   puts k-1, k, i+1, i # こう反転 [abcABC v] ==> [CBAcbav] ==> [vabcABC] ==> [cbavABC] ==> [abcvABC]
   a << v # !! 実際のaはソート済みなので順番覚えず適当に追記しても後で復元できる !!

後ろから解を実行するには、各要素が何番目にあるか、毎ステップ厳密に覚えてないといけません。なので、部分列をとって一部reverseしてくっつけるような処理を書かないとダメ。先頭から解なら、読み込んだとこまではソートされていることが確定しているので、計算中のデータとして厳密に順序を覚えていなくても、なんかデータのカタマリとしてだけ持っておけば処理は回せます。

それと、Ruby で配列の共通部分を計算する & 演算子のように、イマドキの言語では、配列やリストを全体で一つのカタマリとして一気に処理する機能が充実しています。時間計算量で評価するとループと添え字アクセスで要素毎に見えていくのも「一つのカタマリとして演算」も差がありませんが、ゴルフ計算量で評価すると、いかに「全体を一気に」演算に持ち込める形に書くかは重大なポイントとなってきます。そう、逐次実行の時間計算量だけで見てると一見差がないものでも、どれだけ「データ全体を一気に」を有効活用しているかが効いてくるアルゴリズムの世界へ！

おしまい

はい、最後の方適当にこじつけましたスミマセン。

でも、「基本処理のコストがわかってるときに、どう組み合わせたら効率的に問題が解けるか考える」というのが良いアルゴリズムを考える思考の本質であって、そこで基本処理のコスト関数が「実行時間」なのか「コードの長さ」なのかというのは些細な差に思えるなー、と自分が感じているのは本当です。どっちかが楽しめる人は、もう一方もきっと楽しいです。以上！

23:24 11/12/03

論文を読もう

論文というのは、非研究者にとっては、なんかラノベとか漫画とかそういうカテゴリのものであって欲しいと思う。
http://twitter.com/#!/kmizu/status/105660537907593216

論文というと、難しい専門知識が綴られていて、その勉強のために読むもの、というイメージが、もしかしたら、あるかもしれません。しかし世の中には論文読みが趣味という人がいて、そういう人はどちらかというと、ちょっと面白い小話を読んで時間をつぶすためであったり、華麗な技法や証明の紹介を読んで胸躍らせるエンターテイメントとしてであったり、読んだ２分後に忘れててもいいから楽しい時間を過ごそう、くらいの気分で読んでいたりします。いや、２分後に忘れてていいなどと思ってるのは私だけかも知れませんが…。

というわけで、そんな風にみんなが漫画読む気分で論文読む世界を目指すべく、そもそも論文ってどんな感じに見つけたり探したりするのかというお話です。あ、基本的にコンピュータ科学系の英語論文が対象です。

最初の一本に出会う

まず最初に一つ、「面白いな」と思える論文に出会うと、そこを足がかりにすることができます。最初は、まあ、運で、

Twitter を眺めていたら「この論文のイントロが面白すぎる (43RT)」なんてのが流れてた
技術用語でふつーにGoogleなどで検索していたら論文のPDFが引っかかる

くらいでしょうか。論文に特化した検索エンジン（Microsoft Academic Search や Google scholar）もあって、年度を区切って検索する、引用数などの論文の重要度の指標を参照できる、など色々な機能もありますが、科学史上の重要性とか気にして論文読んで何が面白いんだ、と私などは思ってしまいますので、ごく普通の検索エンジンで普通に検索するので十分なんじゃないでしょうか。

良くみかけるドメイン

検索でヒットする論文の載ってるサイトは、研究者の個人ページを除くと、いくつかの出版社などのサイトに限られています。ラノベでいうとレーベルがいくつかあるみたいなものだと思います（適当）。以下にに、自分がよく当たるベスト６の概要を簡単にまとめました。

acm.org と ieee.org には、それぞれ、コンピュータ科学の二大学会である ACM と IEEE から出版された論文が掲載されています。これらの学会の主催する国際会議の発表論文集や、定期刊行の論文誌の論文などがあります。 springerlink.com は、有名な "Lecture Note in Computer Science" シリーズを擁する Springer 社から出版された論文が見つかります。 ACM/IEEE 主催でない会議は、その発表論文集をこのLNCSシリーズで刊行することが非常に多く、かなり多数の会議論文が springer から出ています。 sciencedirect.com は、多数の論文誌を抱える Elsevier 社のサイトで、ページ制限のある会議論文と違って全ての詳細まできっちり書き込まれた論文誌の論文が、多く置かれています。（※注: 逆にSpringerに論文誌もありますし、Elsevierの出す会議録もありますが、なんとなく私が出会う論文の傾向としてはこういうイメージ…）

この４つを始めとする出版社系サイトの論文は、基本的に、有料です。ですが、大学生の人は、もし大学が一括で契約を結んでいれば、大学のIPからアクセスすれば無料で見られるか、大学図書館のプロキシを通すと無料で見られる、という状態になっていることがあります。家で見つけた論文が読めない～と思っても諦めずに、大学から再挑戦してみたり、大学図書館のページをチェックしてみるのはお勧めです。自分はこれを知らずに学部生の頃は諦めまくっていて勿体なかったです。

また、最近は「著者が自分のページで原稿を公開するのは自由」という契約で論文が出版されていることがほとんどなので、多くの研究者が、自分のページでPDFを公開しています。読みたい論文を見つけたら著者名で検索してみて個人サイトを探すのは有効な手段です。

citeseer は、そういった、著者が公開している場合など Web 上に無料公開されている論文をクロールして整理している検索エンジンです。しかしどちらかというと、citeseer 自体を使って論文を探すというよりは、「他の検索エンジンで探したとき元ページより上にランキングされるので見てしまう」「元ページが消えてもPDFなどをキャッシュしていたり、ps形式をPDF形式に変換してくれていたりするので便利」な論文キャッシュサーバとして活用してしまっているかも…。

arxiv.org は、preprint server と呼ばれる、著者が自分のバージョンの論文を公開する場を提供するサービスです。出版された論文の「自分で公開するのは自由」用置き場として使われていることもあれば、もっと早く、会議や論文誌への提出前のアイデアメモみたいな、段階からの意見交換のためにアップロードされているようなPDFもあれば、色々です。個人サイトと違って統一された体裁なので、知らないと出版社サイトのもののように権威のある査読を通った論文と勘違いされてしまうこともあるみたいなんですが、 arxivは誰でも好きにアカウントを取って自分の論文をアップロードできる場所です。なので、P=NP予想を解いたと主張する論文？などは大抵ここに載ってます。といっても、決して逆の勘違いもしないで下さい。決してトンデモ論文置き場ではありません。コンピュータ科学の中だと、特に暗号や計算量理論の方面ではpreprint serverの活用が盛んで、多くの第一線級の論文がarXivで公開されています。国際会議のトップページで、"ページ数制限のないフルバージョンをarxiv等に投稿することを強く推奨" といった文言を見かけることもあります。

次の一本

一つ「面白いな」と思う論文に出会ったら、そこを足がかりに色々探すことができます。私の場合２通りの方向を探しています。

作者買い：同じ著者の書いた別の論文を探して読んでみます。面白い論文を１本書く人をみたら１００本書いてると思え、って、それじゃゴキブリみたいですが、間違ってはいないと思います。例えば私は Conor McBride や Thomas Colcombet のファンなので、新刊を書かさずチェックして追っかけていますが、いつも面白いです。
会議・論文誌買い：面白いなと思った論文が、どの会議で発表されたものか、どの論文誌に出たものかをチェックして、その会議/論文誌の他の論文も探してみます。これも、自分の面白いと思った分野の他の研究が色々見つかってお得です。

これも著者名や会議名で普通の検索エンジンで検索するとだいたい十分ですが、 DBLP という論文データベースサイトがあるので、ここを目掛けて探すのも、かなりお勧めです。例えば、 Knuth先生の論文一覧や CIAAという会議の2011年の論文一覧などなどが見られます。

継続的に

書評サイト、感想サイトを巡って面白い本を探すように、定期的に面白い論文を紹介してくれるブログ等をチェックするのも手ですね。プログラミング言語の話なら Lambda the Ultimate は外せません。理論計算機科学だと、 Theory of Computing Blog Aggregator という記事のaggregatorを見ていると面白いそうです。結構流量が多くて大変なので、私は、その中でお気に入りの Gödel's Lost Letter and P=NP というブログだけは欠かさず読むようにしています。

また、今年は今年読んだ面白CS論文紹介カレンダーというのが12月14日から始まるそうなので、要チェックです！

22:57 11/12/01

自動微分 ≪フォワード・モード≫

最終兵器の名前っぽい。

じゃなかった。突然なんとなく、好きなアルゴリズムの話をしようと思います。私が一番好きなアルゴリズムはヒープソートですが、ヒープソートの美しさは耳で聴けば明らかなので、今回は他の話をしたいと思います。「自動微分 (automatic differentiation)」です。

平方根

昔々、あるところに、こんなプログラムがありました。

template<typename Real>
   Real my_sqrt( Real x )
   {
      Real y = 1;
      for(int i=0; i<100; ++i)
         y = (y + x/y) / 2;
      return y;
   }

特に何の変哲もない、ニュートン法で平方根を計算する関数です。確かめてみました。

#include <iostream>
#include <iomanip>
int main()
{
   using namespace std;
   cout << setiosflags(ios::fixed) << setprecision(9);
   cout << my_sqrt(2.0) << endl;  // 1.414213562
   cout << my_sqrt(3.0) << endl;  // 1.732050808
   cout << my_sqrt(5.0) << endl;  // 2.236067977
   cout << my_sqrt(0.25) << endl; // 0.500000000
}

確かに平方根っぽい値が出ています。ところで、なぜだか偶然、この my_sqrt 関数はテンプレートで書かれているので、実数じゃなくたって、他のどんな型の値を突っ込んでみてもいいですよね。そこで

// 魔法のデータ型
struct dual {
   const double x, dx;
   dual( double x, double dx=0.0 ) : x(x), dx(dx) {}
   dual operator+( const dual& r ) const { return dual(x+r.x, dx*1       + r.dx*1); }
   dual operator-( const dual& r ) const { return dual(x-r.x, dx*1       + r.dx*-1); }
   dual operator*( const dual& r ) const { return dual(x*r.x, dx*r.x     + r.dx*x); }
   dual operator/( const dual& r ) const { return dual(x/r.x, dx*(1/r.x) + r.dx*(-x/r.x/r.x)); }
   static dual var( double x ) { return dual(x, 1.0); }
};

こんなものを投げ込みます。

   cout << my_sqrt(dual::var(2.0)).x << endl;  // 1.414213562
   cout << my_sqrt(dual::var(3.0)).x << endl;  // 1.732050808
   cout << my_sqrt(dual::var(5.0)).x << endl;  // 2.236067977
   cout << my_sqrt(dual::var(0.25)).x << endl; // 0.500000000

メンバ変数 x の方は特にさっきと変わりませんが…もう一つの変数は何かというと

   cout << my_sqrt(dual::var(2.0)).dx << endl;  // 0.353553391
   cout << my_sqrt(dual::var(3.0)).dx << endl;  // 0.288675135
   cout << my_sqrt(dual::var(5.0)).dx << endl;  // 0.223606798
   cout << my_sqrt(dual::var(0.25)).dx << endl; // 1.000000000

はい、d/dx (√x) = 1 / 2√x。

   cout << 1 / (2*my_sqrt(2.0)) << endl;  // 0.353553391
   cout << 1 / (2*my_sqrt(3.0)) << endl;  // 0.288675135
   cout << 1 / (2*my_sqrt(5.0)) << endl;  // 0.223606798
   cout << 1 / (2*my_sqrt(0.25)) << endl; // 1.000000000

元の関数を微分した結果、導関数が計算できています。

もちろん、これは平方根でだけ偶然そうなったわけではなく、＋－×÷ で定義された関数になら、何でも、無造作に double の代わりに dual 型を投げ込めば、元の関数の微分が計算されてしまいます。不思議ですね！＋－×÷ に限定しているのは今回は話を簡単にするために＋－×÷のオーバーロードしか定義してないからですが、例えば標準ライブラリ <cmath> の関数全てに対して dual 型用オーバーロードを適切に定義しておけば、もう、何でも、単に投げ込む物を変えるだけで微分しまくれちゃいます。

好きなところ

計算機で関数の微分を考える有名な方法としては、他に、たとえば、小さな差分を使って近似的に傾きを求める

double d_my_sqrt(double x) {
   return (my_sqrt(x + 1e-6) - my_sqrt(x)) / 1e-6;
}

// だいたい近い値
d_my_sqrt(2.0) // 0.353553347
d_my_sqrt(3.0) // 0.288675111
d_my_sqrt(5.0) // 0.223606786
d_my_sqrt(0.25) // 0.999999000

という手がありますが、精度の問題がつきまといます。どのくらいの差分の値を使えばいいんだろうと考えるのが大変です。自動微分なら、特に何も考えなくても（そもそも有限精度の浮動小数点数を使っているという限界はありますが、その範囲内で）厳密な結果が得られます。これは格好いい。

あるいは、計算式の構文木を受け取って、高校の教科書にあるような微分の公式で別の式に変換という手もありますが、関数としての値ではなくて、内部実装の式そのもの、実装詳細を知らないと微分ができないというのは美しくないと思います。そもそも、forループやwhileループや再帰関数や例外throwやクラスの仮想関数に関する微分の公式がないので、式一個でポンと書ける程度の関数でないと、式変形で微分するのは難しいですね。自動微分なら、単に外から無造作に魔法のdual型を投げ込むだけで、中身の実装は何も考えないで行けます。格好いい。

…いえ、実は、C++ だと元々の関数が double 決めうちで書かれているとお手上げなので、「なんでも無造作に投げ込めば行ける」というのは嘘があります。が、静的型のない言語や、逆に、多相性の表現力の高い型システムのある言語なら、本当に何も考えず投げ込む大作戦は、十分に実現可能です。

※注: といっても、表引きして定数リテラルを引いているような実装には手も足も出ない、というような原理的に難しいケースもありますけれど…

いろいろ

自動微分そのものの仕組みをまったく説明しませんでしたが、 dual 型の定義を眺めているとからくりはわかるんじゃないかと思います。英語ですが、 autodiff.org というサイトが色々な資料をまとめていて面白いので、お暇な方は読んでみてください。お勧めです。

Derive Your Dreams

23:21 11/12/22

「難しい問題」

「名のない関数」

「演算のせいしつ」

21:45 11/12/15

「先延ばし屋の予定帳」

内容紹介

感想

「オートマトンとグリーンの関係の関係」

内容紹介

感想

「ゲーデル先生の抜き打ちテスト」

内容紹介

感想

おしまい

21:48 11/12/09

未来の証明言語を考える

00:01 11/12/07

アルゴリズマーのためのゴルフのススメ

速いは短い

たった１つの変数で

プログラム探索

コードゴルフに大切なもの

パラレルパラレル

おしまい

23:24 11/12/03

論文を読もう

最初の一本に出会う

良くみかけるドメイン

次の一本

継続的に

23:02 11/12/02

歩こう

22:57 11/12/01

自動微分 ≪フォワード・モード≫

平方根

好きなところ

いろいろ