d.y.d.

00:26 12/12/18

BookLive!

7月に出会ってからずっと電子書籍ストアとして BookLive! をひいきにしているのですが、一体どこが好きなのか語りたくなりました。 ITMedia のこれでもう迷わない、電子書店完全ガイドという一連の記事の、電子書籍の端末の話よりストアの話をしましょうよというコンセプトに思いっきり影響されています。

といっても、第一印象が「普通のことが普通にできるので感激した！！」というもので、つまり今年の前半に使っていた幾つかの電子書籍ストア/専用アプリが残念だっただけかもしれません。買った本がどこをクリックすれば読めるのか理解するのに10分かかった、とか、 6冊以上買うと本棚アプリから画面外に本がはみ出るので手でいちいち棚を変えて整理しないと読めない、とか。

本当に普通に使えるという以上に特筆することもないんですが、あ、でも、今年になるまで実感できていなかったことの一つとして、電子書店で「シリーズ」をちゃんと管理してくれているのは便利だなあ、というのがありました。検索結果では常に１シリーズは１項目にまとめて表示してくれて、完結済みなのか途中なのかラベル付けしてくれて、シリーズ画面を開けば全何巻あるのか一目でわかるし、当然まとめ買いもできる、と。

購入すると手元でもやはりシリーズは自動で一つにまとめられて、しかもコンプリートしていないシリーズを開くと

続刊の表紙絵がうっすらと表示されて購買欲を煽ってきます。こういう、ユーザーにとっての得になる使いやすさと、売り手にとって得になる見せ方で双方得させるような UI は格好いいなー、と思いました。こういうシリーズを意識したまとめ方って、国内書店系のストアは程度の差こそあれ大抵のところがやっていて、逆に Kindle や Google のには無いのですよね。手作業でコツコツ細かい所を積み重ねていく感は、なんとなく、それっぽい。

あとは…"スタッフいちおしタイトル" のようなコーナーにちゃんとスタッフのコメントがついて紹介されてるのが、単に本のリストが並んでて何がおすすめなのかわからないストアと比べて好きですね。他店ではパピレススタッフのオススメ日記なんかも良い感じです。

とにかく、電子書籍はまだまだ品揃えが全然足りてない感があって、普段自分が本を買う動機の大きな部分を占めている「Twitterで面白がってる人を見た」や「blogでいい書評を読んだ」ドリブンの購入がほとんどできません。巷で見かけた書名で検索しても、なかなかヒットしない。といって、面白い本の絶対数が足りてないかというとそんなことはなくて、たぶん、今年電子化された本のうち自分に面白く感じられる本のトータル数は、自分が一年で読み切れる量を明らかに超えていると思うのです。つまり、「電子書籍として読める」という条件付きで面白い紹介を流してくれる媒体はとてもありがたく感じます。

つまり、まとめると、良くも悪くも手間暇かかっていて街の「本屋さん」っぽい、ということかもしれません。将来的に全部の本が電子化されるようになって、細かい気配りなしでもどうにでもなる時代になったら、今紙の本なら Amazon で困っていないように、こういう労力って効果が見えにくくなってしまいそうです。が、今、少なくともあと数年の範囲でいうと、こんな気配りはありがたいし便利だし頑張って欲しい。

20:46 12/12/08

＝と ≠ の話

Competitive Programming Advent Calendar Div2012 の参加記事です。

計算量の理論の話で "P＝NP か P≠NP か?" という未解決問題があるのは有名だと思います。「P : 多項式時間で解ける問題全部の集合」と「NP : 非決定性計算というすごいものを使って多項式時間で解ける問題全部の集合」は一致するのかしないのか？少し噛み砕いた説明で、「多項式時間で解ける問題」と「答えの正しさが多項式時間で検証できる問題」は同じかそうでないか、という言い方をされることもあります。

まあ、いずれにせよ未解決です。

今日は、P と NP の話は置いといて、「＝」なのか「≠」なのか、解決済みの問題をいくつか紹介します。

　　　　☆　　　　☆　　　　☆

定理1. 時間階層定理 (Time Hierarchy Theorem) : DTIME(o(f(n))) ≠ DTIME(f(n) log(n))

　DTIME(o(f(n))) = 「f(n) より小さい時間計算量で解ける問題全部の集合」
　DTIME(f(n) log(n)) = 「O(f(n) log(n)) 以内の時間で解ける問題全部の集合」

つまり、

「n³ log n でなら解けるけど n³ より速くは絶対に解けない問題がある」
「n!√n log n でなら解けるけど n!√n より速くは絶対に解けない問題がある」
「2ⁿ でなら解けるけど 2ⁿ / log n より速くは絶対に解けない問題がある」

などと述べています。最後のは言い換えると、「指数時間でなら解けるけど、多項式時間では絶対に解けない問題がある」と言っています。 2ⁿ / log n はどんな多項式よりも遅いので。P ≠ EXP (多項式時間 ≠ 指数時間) ということです。

「使える時間をちょっとでも増やせば、その分だけ、短い時間では解けなかった難しい問題が解けるようになる」という、ものっすごく当たり前の定理のように聞こえるかもしれませんが、それと言ったら P≠NP も同じくらい当たり前な気がしてしまうので、ちゃんと証明できているというのは凄いことです。

あと、この定理では分離帯として log n 倍する必要があるので、もしかしたら、それより小さい幅で時間を増やしても解ける問題は変わらない… DTIME(n²) = DTIME(n² log log n) …なんて現象がどこかで起きている可能性は残されているのかもしれません。

証明のあらすじ:

実際に、「f(n) log(n) 時間で解けるけど f(n) より速くは解けない」問題を具体的に作って証明とします。

入力
　　M: ビット列2つを受け取ってboolを返すプログラム…のマシン語 (=ビット列)
　　x: ビット列
出力
　　M に (M, x) を与えて走らせたら f(M.length + x.length) ステップ以内で true を返すなら、false
　　false を返したり、そのステップ以内に実行が終了しないなら、true

こういう問題。これは、f(n) より速いアルゴリズムでは絶対に解けません。仮に、f(n) より速いアルゴリズムがあってプログラム X として実装したとしましょう。 X(X, X) は f(X.length + X.length) ステップより速く動くわけですが、速く動いた結果 true を返すと考えても false を返すと考えても矛盾します。対角線論法というヤツです。

f(n) log(n) 時間で解ける…かどうかは、実は、「プログラム」や「マシン語」の定義に依存します。例えば「C++を直接実行できる夢のC++マシンのマシン語です!!!!!」と言ってC++のソースコードが書いてあったりしたら、下手すると template の群れをコンパイルするだけで無限に時間がかかってしまって非常に困ります。

逆に、その辺りさえきっちり定義されていれば、この問題の解き方は、

そのマシン語のエミュレータを実装する
それを実際に f(M.length + x.length) ステップ動かしてみる
おわり

です。エミュレートの分のオーバーヘッドがあるので、「f(M.length + x.length) ステップ動かしてみる」ときには f(M.length + x.length) より長いステップ数がかかりますが、それが"解ける"サイドの計算量です。

で、実は時間階層定理は厳密にはチューリングマシンに関する定理なので、この定理が言っていることは、突き詰めると、こうですね。 "log n 倍しか遅くならないチューリングマシンエミュレータをチューリングマシンで書けたよヤッター!!!"

　　　　☆　　　　☆　　　　☆

定理2. 空間階層定理 (Space Hierarchy Theorem) : DSPACE(o(f(n))) ≠ DSPACE(f(n))

　DSPACE(o(f(n))) = 「f(n) より小さい空間計算量で解ける問題全部の集合」
　DSPACE(f(n)) = 「f(n) 以内の空間で解ける問題全部の集合」

"メモリを定数倍しか使わないチューリングマシンエミュレータをチューリングマシンで書けたよヤッター!!!" というわけで、階層定理の、空間計算量（メモリをどれだけ使うか）バージョンです。空間の場合は、時間の場合と違って余計な log n 倍がかかっていないので、つまりオーダーの意味で少しでもメモリ消費が変われば解ける問題のクラスが変わる、と。

「定理」なんて言うと難しそうな感じがしますが、チューリングマシンという変態言語 Esoteric Languageでチューリングマシンエミュレータを書く、しかもできるだけ高速、省メモリなのを書く、という謎の競技と思えば親しみが湧いてきます。 log log n 倍しかスローダウンしないチューリングマシンエミュレータを書いたら歴史に名前が残りますよ！

　　　　☆　　　　☆　　　　☆

定理3. サヴィッチの定理 (Savitch's Theorem) : NSPACE(f(n)) ⊆ DSPACE(f(n)²)

　NSPACE(f(n)) = 「非決定性計算を使って、f(n) 以内の空間で解ける問題全部の集合」
　DSPACE(f(n)²) = 「f(n)² 以内の空間で解ける問題全部の集合」

非決定性の話もしてみましょう。非決定性計算というのは、普通のプログラミング言語に、１個だけ機能が増えたものと思って下さい。すなわち、

if (野生の勘) { ... } else { ... }

というパワフルな機能です。これがあれば、例えばグラフに全ての頂点を一度だけ通る閉路が存在するか調べるハミルトン閉路問題というNP完全問題でも、簡単に解けます。

bool has_hamiltonian_cycle(const Graph& G) {
   Vert v = G.vert[0];  // ここから一周してみる

   set<Vert> visited;
   for(int i=0; i<G.vert.size(); ++i) {
      visited.insert(v);
      bool is_last = i+1 == G.vert.size();

      // 次に進む頂点を野生の勘で探り当てる
      Vert next = null;
      for(Vert u : G.edge[v])
         if( (!visited.count(u) || is_last && u==G.vert[0]) && 野生の勘 )
            next = u;
      if( !next )
        retrn false;
      v = next;
   }
   return true;
}

野生の勘はすごいのです。こういう謎の勘が全部当たると仮定してプログラムを書いて良い、というのが非決定性計算です。正確には

正解がtrueの時には、最高に野生の勘が冴え渡っていれば true を返す。
正解がfalseの時には、必ずfalseを返す。野生の勘がどっちに分岐しようが絶対falseを返す。

というプログラムを書ければ、解けた、ということになります。で、こんなチートありで多項式時間で解ける問題の集合が NP なのですが、それが普通の多項式時間 P より強力かどうかが証明されていない、というのは本当に面白いですね。

さて、話を戻します。NSPACE(f(n)) ⊆ DSPACE(f(n)²) です。これは、野生の勘ありで f(n) のメモリ消費で解ける問題は、なしでも f(n)² で解けると言っています。これは凄いことで、n の替わりに n² 使えば解ける、 n³ の替わりに n⁶ 使えば解ける、多項式なものはちょっと次数は増えるけど多項式で解ける、と言っているので、時間に関しては未解決 P =? NP ですが、空間計算量に関しては PSPACE ＝ NPSPACE が示されているということです。

証明のあらすじ:

要は、f(n) 空間で動く非決定性プログラムが与えられた時に、その結果を f(n)² 以内の空間消費で計算して返す普通のプログラムを書けばよいのです。

これは基本的には、グラフの探索問題と考えることができます。非決定性とはいえメモリを f(n) ビットしか使わないので、計算途中の状態は高々 2^f(n) 通りしかありません。普通のプログラムだと状態は一直線ですが、野生の勘 のせいで、各状態からは２本の辺が伸びることがあります。そういうグラフで、「初期状態から、"trueを返す状態"の間にパスがあるかないか判定せよ」という問題です。 2^x 個の頂点があり、頂点1個を表現するのに x メモリを使うグラフの、２点間の到達可能性を O(x²) のメモリ消費で判定せよ という、純粋なアルゴリズムの問題に帰着されました。

当然ながら、指数個の頂点があって、パスの長さも指数になる可能性があるので、単純に深さ優先探索や幅優先探索をすると、指数オーダのメモリを使ってしまいます。これには真ん中で割って分割統治する、という典型手法があって

bool is_connected(Graph g, Vert s, Vert t) {
  return is_connected_in_N_steps(g, s, t, g.vert.size());
}

bool is_connected_in_N_steps(Graph g, Vert s, Vert t, int N) {
  if( n == 0 ) return s == t;
  if( n == 1 ) return g.edge.has(s, t);
  for(Vert m : g.vert)
    if( is_connected_in_N_steps(g, s, m, N/2) && is_connected_in_N_steps(g, m, t, N-N/2) )
      return true;
  return false;
}

こうすると再帰の深さは log 2^x = x ですし、再帰の各関数では定数個のノードしか保持していないので、全体で O(x²) のメモリ消費になります。この真ん中で割って再帰という方法は、競技プログラミングな方向だと、最長共通部分列 (LCS) を求める DP のメモリ消費を O(n²) ではなく O(n) に抑える手法などとして使われます。

　　　　☆　　　　☆　　　　☆

と、そんなところで。他には Padding Argument を紹介しようと思っていたんですが長くなったのでやめます。ぜひ Wikipedia を見て下さい。明日は uwiさんの番です！

23:43 12/12/01

汎用ソート殺し

前回の日記（３ヶ月前！）を書いた後、こんなものを作っていました。

Devils and Angels

要するに、ソートアルゴリズムの可視化です。IE9 と Firefox20 と Chrome24 では動いているようでした。どのように見せているかというと、ソートの途中で値と値を比較して大小関係がわかったら、線で結んで大きい方を上に動かします。

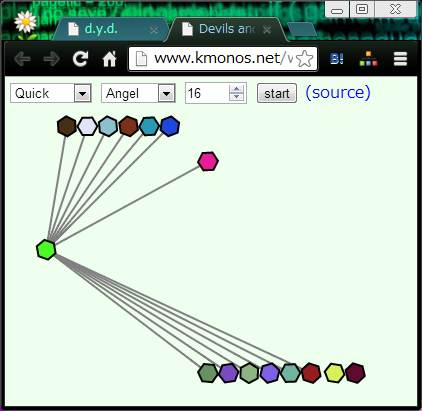
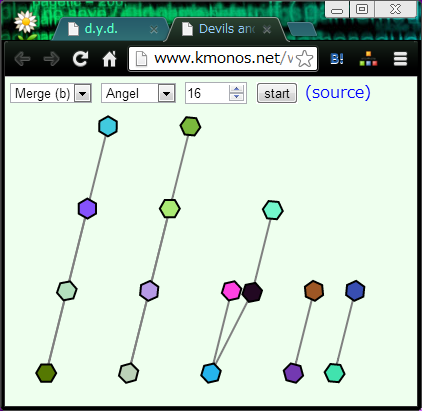
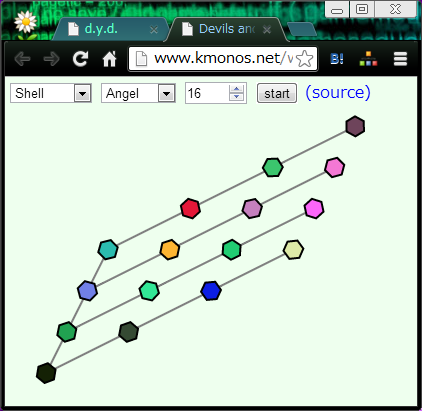
（図はクイックソート・マージソート・シェルソートの途中。）

"Angel" を選ぶと、接待モードに切り替わって、対象のソート法が一番得意とする並び方のリストを渡すようになります。クイックソートだったら、なぜか常に pivot がちょうど真ん中の値を引き当てます。逆に "Devil" を選ぶと意地悪モード、悪い方悪い方のリストをソートさせるようになります。

で、ちょっと面白いと思うところが、この "Angel" と "Devil" を自動生成しているところです。ソート関数が

// array : ソートしたい配列
// cmp   : ソート順序を決める比較関数。aがbより小さいならcmp(a,b)はtrueを返すこと。
function sort(array, cmp) {
  ...
}

こんな感じで比較関数を取る形で実装されてさえいれば、

sort([0,1,2,...], function(a,b){
  // 自分がどのように呼び出されたかの履歴を記録・解析して、
  // そのアルゴリズムの最悪/最善ケースを見つけ出すスパイ関数
});

こういうことをして、例えば「挿入ソートの最悪ケースは逆順ソート済みの時だから…」のように予め人間が手でデータを用意せずとも、全自動で、各アルゴリズムにとっての極端なデータを作ることができます。つまり実装を全然知らなくても実行環境の Array.sort に対してもできる限りの嫌がらせができるということです。

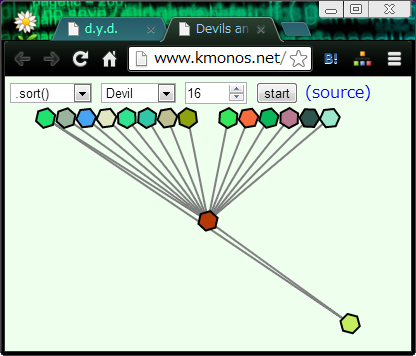
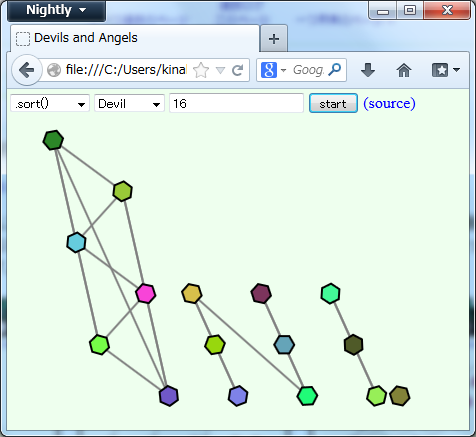
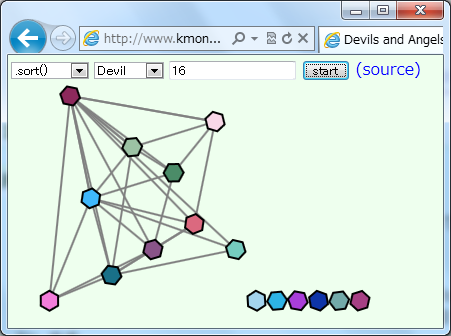
動かしてみたところ Chrome は最初に3点取った中点をpivotにするクイックソートっぽいんですが、 Devil にすると当然、最初に取った3点に最小値と二番目に小さい値がなぜか含まれてしまいます。
Firefox はマージソートのようですが、マージする際に最初だけ片方の最大値をもう片方の最小値と比較することで、ソート済みの時にマージが一瞬で終わる工夫がされています。って、今回のビジュアライザ作るまで私はそんなことは知りませんでしたが、これも勝手に効果的にDevilさんが潰しにいきます。（といってもマージソートなので O(n log n) の範囲は超えられないのですが。）
IE はこの程度のサイズなら挿入ソートで済ませるようです。ただし、挿入箇所を二分探索で決めているようで、Devil にすると複雑な形ができあがります。面白いですね。

この、比較関数にソートキラーを突っ込むという手法は A Killer Adversary for Quicksort がネタ元で、ただこちらはクイックソート殺し限定（まずpivotを選ぶはず、という性質を利用して最初の方の比較では最小値を比較させるらしい）のようだったので、一般化を考えてみた、というのが工夫したところです。

方法

といっても大したことはなくて、上下関係が未確定の比較をするように言われたら、「＜」と答えたときと「＞」と答えたときでどちらが情報量が大きいかを計算して、 Devilなら情報量が小さい方、Angelなら大きい方を答えています。

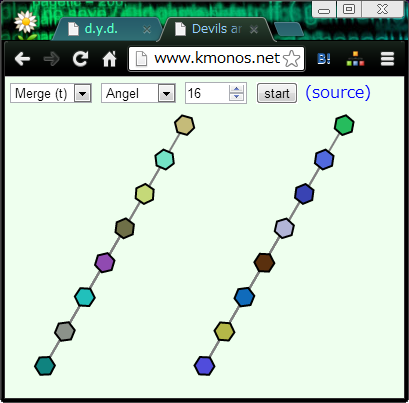
たとえばこの例で、「左のチェインの最大値＜右のチェインの最小値、ですか？」とソートアルゴリズムさんが聞いてきたとしましょう（Firefoxの挙動です）。ここで「＜」と答えると、そのペアの大小関係だけではなくて、それに付随して「左のチェインの値はどれも右のチェインの値より小さい」が確定してしまうので、 8×8 = 64 ペアの大小関係が暗黙に決まってしまいます。逆に「＞」と答えれば 1 ペアしか決まりません。というわけで、Angel さんは前者を答え、Devil さんは後者を答えます。

ちゃんと証明してないですが、「制約を満たす並び替えの可能性の総数」の増減で情報量を定義するのが多分本当だと思いますが、それと確定ペア数での議論は一致するはず…たぶん。非連結な部分を連結するパターンのときだけ証明して力尽きたので誰かやって下さい。

あと、これが真の「最悪」を選べるのか、というとそんなことはなくて、極端な話、「初めはクイックソートで開始、初手10手がクイックソートの最悪パターンと一致していたらマージソートに切り替え、そうでなければバブルソートに切り替え」みたいな変なことをされた時に、最悪はバブルソートに落とすことですがそれを選ぶのは無理です。

まとめ

まとめらしいまとめは特にないんですが、つい最近シェルソートの計算量を理解しようと思ったときにこの可視化がとても理解の助けになったので、自分としては作ってよかったなあと思いました。

目下最大の問題点は

ソート処理に比較関数渡してその呼ばれ方から自動で最悪例を作るgeneric sort killer、作ったはいいけど、まず最悪例を作ってる最中に最悪例を自ら踏むので最悪例作成処理が時間かかりすぎて帰ってこない
http://twitter.com/kinaba/status/243358049044164608

これで、比較のたびに確定関係のグラフをたどって全ペアの影響を数えてるので、動作に
　　O(ソート自体の計算量 * n^2)
時間かかってしまうのです。どなたか高速化して下さい…。

追記: O(n^3 + ソート自体の計算量) までは落とせました。

Derive Your Dreams

00:26 12/12/18

BookLive!

20:46 12/12/08

＝と ≠ の話

22:15 12/12/03

最近はまってるゲーム

23:43 12/12/01

汎用ソート殺し

方法

まとめ

Derive Your Dreams

00:26 12/12/18

BookLive!

20:46 12/12/08

＝ と ≠ の話

22:15 12/12/03

最近はまってるゲーム

23:43 12/12/01

汎用ソート殺し

方法

まとめ

＝と ≠ の話