d.y.d.

09:25 10/12/31

年末まとめ

今年何やったっけ、と日記を読み返していました。何もやってないな…。 Polemy 作りました、くらい。言語処理系作るのはやっぱり楽しいですね。汎用言語として使う本格的なものを作ろうとすると懲りすぎて一歩も進まなくなってしまう自分が見えるので、来年は、そうだなあ、TopCoder/ICPC風コンテストに特化した言語というかC++へのトランスレータ、くらいに絞って作ってみようかなあ。書いた記事だと最短性チェックの話が自分では割と気に入っています。これのもっとバグを許容するバージョン作れないか。読んだ論文で面白かったのは "A Pearl on SAT Solving in Prolog" と "When Simulation Meets Antichains" (PDF) など。

あとは、今年読んで面白かった本ベスト５（順不同）：『カモ少年と謎のペンフレンド』海の向こうとの文通、という青春物かと思いきや、相手の様子があきらかに常軌を逸している、そしてそれをすべて承知の上でその異様さに取り込まれていく少年…というオカルトかと思いきや…と二転三転して、最後に見事に伏線を回収して着地。子供向けの作品なのだそうですが、作中で引用される物語をとても続きが気になるやり方で切って紹介していて、あざといといえばあざといんだけど、面白い本をもっと読ませたい、という愛が伝わってきて楽しかった。『ボクらのキセキ』未来の恋人を名乗る者からの「僕たちは出逢ってはいけない、さもないと人を殺してしまうことになる」という電話…から始まる、これもファンタジーなのかラブコメなのかミステリなのかジャンルを決めずに転がりまわる系のお話。結末は正直イマイチかもと思わなくもなかったですが、このめまぐるしく展開する過程が私は好きすぎるのです。あと、文章/文体が綺麗でよいと思う。『俳句』初心者の句15万を集めてダメな部分を分類してまとめたので、読者諸君はこの罠はさっさと全部切り抜けて先へ向かいたまえ、という、異彩を放つ一冊。主張の是非を判断できるほど僕は俳句に明るくないのですが、それでもわかるのは、とにかく論旨が異様に明確。俳句とは、自らの内に起こる心の動きを、「具象の言葉のみを用いて」、聞き手の心にその動きを再現させるフレーズとして凝結させたものである、と、目が覚めるほどはっきりしている。あと何となくコードゴルフっぽいと思った。『ギャルゲヱの世界よ、ようこそ！』今年は、ゲームの世界の中に入っちゃう系のお話を集めて色々読んでいたのですが、主人公が(MMO)RPGの中に入っていく話が多い中で、ギャルゲーの登場人物や設定が現実に投影される、という逆向きの設定をとったこの作品が頭三つ抜けて面白かった。初めはゲーム内通りのラブラブハッピーな展開でスタートするんだけど、どうしても架空のシナリオなので "無理がある"。（典型的なのは、分岐選択の結果選ばれなかったヒロインは恐ろしく不幸な末路を辿らざるをえない設定になっちゃってるよね、というよく議論されるネタだけど、当然それだけでは終わらない。）その無理を是正するために否応なく、 "現実が仮想世界に"ではなく、"仮想世界が現実に"少しずつ侵食されて崩れていく、という構成はよくよくできてると思います。『時空と大河のほとり』の中の一編、『時の破片』。古代の陶器から"音"を再生する、というキーアイデアが、現実性はともかく夢があって面白いなあ、と感激しました。これぞ Science で Fantasy。音響考古学などというらしい。

そんなところで。では、良いお年を！

22:55 10/12/29

メタプログラミングの会

もう３週間以上前ですが、メタプログラミングの会というのに混ざってきました。思い出したように参加記。

聞いた発表の中では、herumiさんのXbyakの話が面白かったです。テクニカルな話としては知っている内容ではあったのですが、見方として面白かった。 JITで実行時に機械語生成できるとかそういう部分もあるけれど、とにかく、超高度なマクロアセンブラというか、 C++ の制御構造をフルに使ってアセンブラ書けるという点を重宝している、というのが、なるほどなーと。

自分は、『プログラミング言語 Polemy』というネタで喋ってきました。「こんな言語があったら面白そうな気がするけど、仕様の詳細どうすると整合性がとれるか, 作ってみないとさっぱりわからんなー」と前に思ってたものを、せっかくの機会だし、と作ってみたものです。どんな言語化はスライド (PDF) やリファレンスをご覧下さい。マクロなどは Syntax をできるだけユーザーが好き勝手に定義できるようにする指向だと思うんですが、 Semantics をできるだけユーザーが好き勝手に定義できる指向のようなものを漠然と考えていました。

作ってみてわかったのは、りりかるろじかるさんの eval に評価機を指定できる言語、というまとめ方がわかりやすかったのでこのたとえを拝借すると、まだ first class さが足りないなーという辺りですね。「実装にはこのレベルの計算を使ってね」だけなら

fun(@type x){ @type(x) } # 型レベルで eval

とか関数でラップすれば擬似的にできるんですが、それ以上のことをやろうとすると、困るのが、eval の呼び出し部分が完全に組み込みになってしまっていることで、今の仕様だと eval を eval 以外の意味で解釈できなくて結構不便。これは暇なときに続きを考えてみたいと思います。

00:07 10/12/23

std::rotate を読んでみた

STLの面白い関数の実装を読んでみるシリーズ第２回兼最終回。

string s = "1234ABCDEF";
std::rotate( s.begin(), s.begin()+4, s.end() );
std::cout << s << std::endl; // ABCDEF1234

配列やリストなどのデータ列を、指定した位置が先頭にくるようにクルッと回す関数 std::rotate です。

単純な処理に見えますが、余計なバッファを確保しないでこれをやろうとすると、かなり頭の体操になります。「まず A を 1 の所にもってきて、1 は E のところに動くからそこに入れて、すると E を追い出して E の行き先は…」あたりで私の頭は力尽きました。 libstdc++ のソースコードを参考に、どうやってるか理解してみよう。以下、自分なりに理解しやすいように書き直してみたものです。

template<typename FwdIt>
void f_rotate( FwdIt s, FwdIt m, FwdIt e )
{
  if( s==m || m==e )
    return;

  // 例として、入力データが [１２３４ＡＢＣＤＥＦ] で
  //   s[１２３４]m[ＡＢＣＤＥＦ]e 
  // こんな風に s, m, e が位置を指していたとする。

  FwdIt original_middle = m;
  while( s!=original_middle && m!=e )
    std::iter_swap(s++, m++);

  // まず s と m を swap しながらできるだけ右に進めると、こうなる
  //   [ＡＢＣＤ]s[１２３４]m[ＥＦ]e 
  // ＡＢＣＤ 部分は完成したので、残りを再帰的に rotate

  if( s == original_middle )
    f_rotate( s, m, e );
  else
    f_rotate( s, original_middle, e );

  // ↓こうなる。完成。
  //   [ＡＢＣＤ][ＥＦ１２３４]
}

ForwardIterator 汎用ルーチン。イテレータを ++ で進めることはできるけど -- やランダムアクセスは使えないとき。末尾再帰なので簡単にループに直すことができて、実際には while ループで実装されています。 s と m が 1 歩ずつ右に進んで行って、区間の長さはユークリッドの互除法（互差法？）的に縮んでいくので最大公約数のところで終わるので、 (e-s) - gcd(m-s, e-s) 回 の iter_swap が必要。

次は ++ と -- が使える BidirectionalIterator の場合。この場合 std::reverse で順序逆転ができる。

template<typename BidIt>
void b_rotate( BidIt s, BidIt m, BidIt e )
{
  if( s==m || m==e )
    return;

  // s[１２３４]m[ＡＢＣＤＥＦ]e 

  std::reverse( s, m );
  std::reverse( m, e );

  // まず両側を逆順に並び替える。
  //   s[４３２１]m[ＦＥＤＣＢＡ]e 

  while( s!=m && m!=e )
    std::iter_swap(s++, --e);

  // 左端と右端を swap しながら、m にぶつかるまで区間を縮めていく
  //   [ＡＢＣＤ]sm[ＦＥ]e[１２３４] 
  // こうなる。左側と右側は完成したので、あとは真ん中を元に戻せばよい。

  if( s == m )
    std::reverse( m, e );
  else
    std::reverse( s, m );

  // ↓こうなる。完成。
  //   [ＡＢＣＤ][ＥＦ][１２３４]
}

最初の reverse が (m-s)/2 回、次のが (e-m)/2 回の iter_swap。次の左右 swap が min(m-s, e-m) 回。最後の reverse が (max(m-s, e-m)-min(m-s, e-m))/2 回。合計すると… (e-s)/2 + (max(m-s,e-m)+min(m-e,e-m))/2 だから、結局 e-s 回、って、あれ？回数増えてないですか。勘違いしてるかな…。

ちなみに Visual C++ 2010 付属の STL の実装はもっと豪快で

template<typename BidIt>
void b_rotate( BidIt s, BidIt m, BidIt e )
{
  // s[１２３４]m[ＡＢＣＤＥＦ]e
  std::reverse( s, m );
  std::reverse( m, e );
  // s[４３２１]m[ＦＥＤＣＢＡ]e 
  std::reverse( s, e );
  // [ＡＢＣＤＥＦ１２３４] 
}

これも (m-s)/2 + (e-m)/2 + (e-s)/2 = e-s 回。これは目から鱗が落ちました。左右から迫りながら iter_swap って、言われてみれば確かに reverse 操作なので、全部 reverse でいいじゃない、と。美しい。

RandomAccessIterator の場合、 0 番目に m-s 番目を入れ、m-s 番目に 2(m-s) 番目を入れ、と玉突き的にずらしていく手が可能になります。この玉突きは一周では終わらなくて、0 番目から始まる玉突きサイクル、1 番目サイクル、……、 gcd(m-s, e-s)-1 番目サイクル、まで回すと終了。 Juggling Algorithm というらしい。

template<typename RndIt>
void r_rotate( RndIt s, RndIt m, RndIt e )
{
  if( s==m || m==e )
    return;

  typedef std::iterator_traits<RndIt>::difference_type Index;

  // 例: [１２３４ＡＢＣＤＥＦ]

  Index G = __gcd(m-s, e-s); // 最大公約数(4,10) = 2
  for(Index i=0; i<G; ++i)
     for(Index cur=i, next; (next=(cur+(m-s))%(e-s)) != i; cur=next)
       std::iter_swap( s+cur, s+next );

  // [１２３４ＡＢＣＤＥＦ]
  //   ループ１周目(i=0) では 0←4←8←2←6←0 と玉突きして
  // [Ａ２Ｃ４ＥＢ１Ｄ３Ｆ]
  //   ループ１周目(i=1) では 1←5←9←3←7←1 と玉突きして
  // [ＡＢＣＤＥＦ１２３４]
}

かくサイクルで、(サイクルの長さ - 1) 回ずつ iter_swap が呼ばれるので、合計 ((e-s)/gcd(m-s, e-s) - 1)*gcd(m-s, e-s) = (e-s) - gcd(m-s, e-s) 回 でした。

少なくとも iter_swap の呼び出し回数だけ見ると、一番最初の ForwardIterator 版１つでいいんじゃないか…という気がしてしまうのですが、定数倍の違いで後で紹介したバージョンの方が速かったりするのでしょうか。それともやっぱり私が勘違いしているかなぁ…。今度ベンチマークでも取ってみよう。

23:00 10/12/21

正規表現しちへんげ！　まとめ

正規表現の特徴付けを紹介するシリーズ。

以上です。他にも持ってこようと思えば色々あると思うんですが、あんまり面白いものが思いつかなかったので、この辺りで打ち止めです。全体を通して 有限性 / 周期性 / 線形性 のような現象、というのが特徴となっているんじゃないかなぁという気がします。

面白いのは面白いんだけど、このシリーズの中でどうやって紹介したものだろう…と思って結局できなかったものが二つあって、一つは [Rutten 98] "Automata and Coinduction (an exercise in coalgebra)" などなどの「正規言語を余代数（coalgebra）の視点から扱う」話。 Rutten の論文では、余帰納法 (coinduction) や双模倣 (bisimulation) といった証明技法がいかに綺麗にハマるかが整理されて紹介されています。日本語の記事では余代数と余帰納法 - ヒビルテなど。

もう一つは [Schützenberger 61] "On the Definition of a Family of Automata" 以降の、形式ベキ級数を使った表現。文字を変数と思って、a+ab+abb+abbb+abbbb+... という多項式のような、係数は1か0だけ取れる項の無限和を {a,ab,abb,...} という集合と見なす、という見なしで、正規言語に限らず言語を扱います。ベキ級数同士の足し算や掛け算を、多項式の演算と同じように定義すると、なんとなく上手く行く感じ。 * もそれっぽく、1/1-x = 1+x+xx+xxx+... を念頭に置くと格好いい書き方ができることがあります。係数を {0, 1} から一般に自然数にしたり実数にしたりすることで、文字列に色々な重みをつけた状態へと、統一的に一般化した議論ができたり。色々。

18:00 10/12/21

正規表現しちへんげ！　最終夜

正規表現は、違う書き方をしてもまったく同じ文字列にしかマッチしないことがあります。

さて、二つの正規表現が与えられました。例えば、何も考えず書いたバージョンと、最適化して綺麗に効率よく処理できるようにし直したバージョン。同じ言語を表しているはずなんだけど…というときに、それが同じなことを証明するにはどうすればいいでしょうか。はい、「Kleene代数の公理系」というものを使います。

x|(y|z) = (x|y)|z
x(yz) = (xy)z (結合則)
x|y = y|x (交換則)
x|x = x (冪等性)
x(y|z) = xy|xz
(x|y)z = xz|yz (分配則)
x|0 = x
0x = x0 = 0
1x = x1 = x (単位元)
1|xx* ⊆ x*
1|x*x ⊆ x*
x|yz⊆z ならば y*x⊆z
x|yz⊆y ならば xy*⊆z (*の性質)
以上の公理で、正規表現の同値性は全て証明できる

Perl などで使われる正規表現だと ( ) でその部分マッチをキャプチャできたりしますけど、そういうのは考えないで、括弧は単に演算子の結合を変えるだけということで、同値性を考えています。 0 何にもマッチしない正規表現、1 は空文字列にだけマッチする正規表現を表します。 x⊆y は x|y=y の略記。

この公理系は導出できた等式は必ず実際に成り立ち、逆に実際に成り立つ等式は必ず導出できることがわかっています。いわゆる、健全で完全な公理化。自然数論を含む理論ではそれは不可能なのは有名な話ですが、正規表現にはそこまでの表現力がない（…ここまで幾つもの定義に出てきたように、とにかく有限状態で、線形関数なものしか表現できない…）ので、できます。

できますといっても簡単にできるわけではないらしく、この完全な公理系ができてからまだ16年しか経っていないくらいです。基本的に、「DFAを作る → 状態数を最適化する → 完全一致するか調べる」というアルゴリズムで正規表現の等価性はわかるのですが、この方針を、上のシステムなら１ステップ１ステップの証明としてエンコードできるのだとか。

応用

等値性の証明を、DFA経由に頼らずこの公理系のような導出規則で表現しておくと、それを証明の証拠として外部に送ってやりとりして検証に使えたり、証明から自然に、マッチ結果の構文木の変換アルゴリズムが抽出できたり、色々できるよ、という話が今度の POPL 2011 に出る論文で論じられていました。

というわけで、クリスマスには少し早いですが、今回が最終回です。あとで目次エントリあげます。

文献： [Kozen 94] "A Completeness Theorem for Kleene Algebras and the Algebra of Regular Events"

21:00 10/12/20

正規表現しちへんげ！　第十六夜

準備が必要です。

weakly commutative

po(y₁, y₂, …, y_n) を、「yを2個選んで順番入れ替え」を奇数回繰り返してから順番に結合して作れる文字列全体の集合（奇置換）、 pe(略)を(略)偶数回(略)、とします。文字の集合 L が n-弱可換 であるとは、どんな文字列 x, y₁, y₂, …, y_n, z を取ってきても、「x po(y₁, y₂, …, y_n) z のうち L に入る文字列の数」と「x pe(y₁, y₂, …, y_n) z のうち L に入る文字列の数」が等しいことを言います。

何を言っているかわからないかもしれませんが、安心して下さい。紹介している私も実はあんまりよくわかりません。「2-弱可換」は「可換」とも呼ばれ、要するに、文字をどう並び替えても L に入るか入らないかが分からない、文字の順番関係ない言語になります。十分大きな n を決めれば n-弱可換になる言語のことを、単に「弱可換」と言います。

periodic

「どんな文字列 x でも、うまいこと自然数 a と b を選ぶと、 x^a (xをa回くり返した物) と x^b が第七夜の意味の同一視で同じものになる」ような言語を、「周期的」であるといいます。第七夜の有限性が正規言語の定義だったので、少なくとも、正規言語は全て周期的です。周期的だとかなり正規言語っぽい。でも、確実に正規言語かというとそんなことはなくて、追加の条件が必要です。それが…

定理

弱可換 & 周期的＝正規言語

「周期的」が正規言語っぽい、というのは割とよく知られた事実だと思います。繰り返しは * なので、正規言語なら、長い文字列は同じものを繰り返し繰り返して作るしかない。一方で、「弱可換」というのもこれまた正規言語っぽい性質みたいですね。２つ合わせるとピッタリ正規言語を定義します。しかし、弱可換の方って、直感的に一言で気分を理解しようと思うと、どういう概念なんでしょう、これは。

さて、次回が最終回です。まだアレがないだろアレが！と思った人は是非是非、記事書いて下さい。

文献： [Reutenauer 81] "A New Characterization of the Regular Languages" (有料)

17:00 10/12/19

正規表現しちへんげ！　第十五夜

準同型ふたたび。この前は長々と説明しましたが、文字列に限定するなら「concatMap で書ける String -> String の関数＝準同型」でいいんじゃないのだろうか、ということにさっき気づきました。それはさておき。

S を正規表現 a*b の表す言語とする。つまり S = {"b", "ab", "aab", "aaab", ...}
f, g, h を文字列から文字列への準同型（第三夜参照）とする
f(g^-1(h(S))) は正規言語。この形で書けるものだけが正規言語

^-1 は逆写像です。S にマッチする文字列を h で変換して、g で逆変換 (gを適用したら目的の値になるような入力を適当にとってくる)して、h で変換、で作れる文字列全体の集合 f(g^-1(h(S))) = {w | x∈a*b, h(x)=y, y=g(z), f(z)=w} は正規言語だし、全ての正規言語はこの準同型３個の形で作れる、と言っています。

こう書いたら常に正規言語になる、という方は割と当たり前で、逆の、どんな正規言語もこう書ける、という側が重要です。つまり感覚的には、正規言語の持ってる表現力、その特徴的な部分というのは a*b というシンプルな正規表現に全て凝縮されていて、あとはちょちょいのちょいっと変形すれば作れる、と。

こういう「特徴を凝縮した言語」は正規言語に限らず他の言語クラスにもあって、例えば The Hardest Context-Free Language というのは対応のとれた括弧が並んでる隙間に、煙幕のように余計な括弧が大量に非決定的に紛れ込んでる言語で、全ての文脈自由言語は h^-1 (HardestCFL) と、準同型の一撃で作れることがわかっています。準同型は線形時間で計算できるので、この結果を使うと、たった一つの言語、HardestCFL さえ高速に構文解析できれば、他の全ての文脈自由言語が高速に構文解析できるみたいなことが言えます。

「文脈依存言語」や「チューリングマシンで判定可能な言語」にも準同型の逆変換１発で全てを生み出せる Hardest 言語があることがわかっていて、正規言語だと３発必要（２発では無理なことが証明されています）というのが、むしろちょっと不思議な感じです。

文献： [Latteux & Leguy 83] "On the Composition of Morphisms and Inverse Morphisms" (有料)

20:00 10/12/18

正規表現しちへんげ！　第十四夜

文字列と文字列の間の「距離」を考えます。「似て」れば似てるほど「近い」と定義します。

文字列 s と文字列 t に対して、これを区別できる（sは受理するけどtは拒否、またはその逆）最小の DFA のサイズを m(s,t) とする。
文字列間の距離を d(s, t) = 2^-m(s,t) と定義する。
この距離に関して完備化した空間での"閉かつ開"集合（のうち普通の文字列だけ残した部分集合）＝正規言語

a⁶⁰ ("a"が60個並んだ文字列) と a⁶¹ は、長さ偶数の文字列だけ受理する 2 状態の DFA で区別できるので、距離 0.25。かなり遠い。a⁶⁰ と a¹²⁰ は区別に 7 状態も必要なので、距離 0.0078125。わりと近い。そんな距離です。

完備化というのは、距離を定義すると「収束」が定義できるんですが、その時の収束先が元の集合に入ってなかったら足しまくるという操作です。例えば有理数全体の集合を完備化すると、1, 14/10, 141/100, 1414/1000, 14142/10000, ... という数列の収束先 √2 が有理数じゃないので、これを新しく追加！…とやっているとそのうち実数が全部入って、有理数全体を完備化すると実数全体になります。

開集合・閉集合というのは普通の距離の場合と同じで、境界上にある点をまったく含まないのが開集合。「3未満の数全部」みたいな、端を含まないもの。閉集合は逆に「3以上の数全部」のような端を全て含むもの。閉であり同時に開、というのは普通の空間の距離だとあんまり無いですけど、要は、そもそも「境界」がない「数全部の集合」や「空集合」などですね。

色々

この定理は、DFA という正規言語を認識できるデバイスは既にあるものとして、それの上で何かを言っているわけなので、これ自体が正規言語の性質を直接言い表しているものではありません。と思います。たぶん。おそらく。DFAじゃなくても適切な言語認識マシンを適切に計った値を使えば類似のことが言えそう。たぶん。

それよりは、これは、こういう「距離」を考えてみて完備化した世界から文字列を眺めてみよう、という見方の提案になっています。少なくとも「正規言語」が距離空間・位相空間の最重要概念である閉集合・開集合と結びつくことがわかったので、そこを足がかりに位相の世界の言葉で覗いてみると、正規言語さんのことがもっとわかるのでは…という狙い。

もっと直感的な距離である d(s,t) = -2^{(s,tの共通接頭辞の長さ)} を入れて完備化すると「無限文字列」が出てくるんですが、そちらの方が有理数から実数を出すのに近くて、今回のDFAのサイズで距離を入れる方は、無限文字列とはまた違う「Profinite(射有限?)文字列」という物体を生み出します。整数論などで使われる p進数の文字列バージョンとなっているそうです。

文献： [Hunter 88] "Certain Finitely Generated Compact Zero Dimensional Semigroups"
文献： [Pin 09] "Profinite Methods in Automata Theory"

21:00 10/12/17

正規表現しちへんげ！　第十三夜

第十一夜の、「NFA の OR を XOR にしてみた」という正規言語の定式化を見て、誰もがこう思ったのではないでしょうか。

　「じゃあ『AND にしてみた』は無いの？」

あります。しかも、もうめんどくさいのでブール演算全部できるようにした、しかも一文字読むごとに毎回できるようにしました。

Q = "状態"の有限集合
E = Σ×Q から、Q の要素を変数とするブール論理式への関数
I = Q の部分集合
F = Q の要素を変数とするブール論理式
が存在して、I に属する状態から E に従ってたどって、F を満たすようにできる文字列
という形で表せるものが正規言語

NFA だと、要するに F としては q1 OR q3 OR q5、のような OR 式しか書けなかったわけです。 NXA なら、q2 XOR q4、などなど。ここで大盤振る舞い、NOT (q1 AND q3) XOR q4 でも何でも好きに書いてOK！というのがAFA。一歩一歩の進み方を決める E の方もブール式が書けて、例えば E('a', q) = q1 AND q2 だったら、「ここまでの文字列を読んだら q1 にも行けるし、かつ、q2 にも行ける、なら、次の文字が'a'の時は q に行ける。」と、ここもブール論理式で条件を書けます。

AFA (Alternating Finite Automaton) と言います。 Alternating (交代) っていう名前がついているのは何で？と思ったかも知れません。この定義はあんまり交代っぽくないのですが、 Wikipediaにある定義の一つ目はもうちょい交代っぽいです。 AND だけが使えるフェーズと OR だけが使えるフェーズが交互に来るオートマトン。将棋やオセロのAIの探索木みたいなイメージですね。

使い道

ここまでやっても、表現力は正規言語と変わらないのです。これも、Powerset Construction で普通のオートマトンに変換することができちゃう。では何故こんなものを考えるかというと、「AND や OR や NOT を計算するのが簡単だから」です。 DFA や NFA だと、状態や遷移関数をごっちゃごっちゃと変換しないといけませんが、 AFA なら遷移の論理式に AND や OR をそのまま書くだけ。特に論理式をDFAに変換の時のような、仕様を正規言語の枠組みに落とし込むときには、途中の計算は全て AFA でやって、最後の最後だけ必要なら DFA に変換、というような中間データ構造として活躍します。

文献： [Brzozowski & Leiss 80] "On Equations for Regular Languages, Finite Automata, and Sequential Networks" (有料)
文献： [Chandra & Kozen & Stockmeyer 81] "Alternation" (有料)

22:00 10/12/16

正規表現しちへんげ！　第十二夜

たまには突飛なことを書かないと飽きそうです。えいや。

連立一次方程式の解　＝　正規言語

突飛すぎましたスミマセン。説明します。

ax + by + c = x
bx + cy = y

という「方程式」を、例として考えます。x と y が未知変数で、a と b は係数。変数や係数は、文字列の集合 を表します。a は要素が１個だけの集合 {"a"}。b は {"b"}、c は {"c"} を表します。掛け算を文字列結合、足し算を集合の和集合演算と思った時、この連立方程式の「解」はなんでしょう？答えは

x = (a*(bc*b)*)*c
y = c*b(a*(bc*b)*)*c

という正規言語です（気になる人は確かに式が成り立つことを確認してみて下さい。もしかしたら私も計算間違ってるかも。 ※追記：間違ってました修正(23:58)大修正(0:04)）。

こんな風に、定数×変数＋定数×変数＋...＋定数×変数＋定数＝変数の形のを立てると、その解は必ず正規言語になります。逆に、どの正規言語も、必ずこの連立方程式の形で書けます。理由はわりと当たり前で、これは要するに右線形文法をちょっとファンシーな形で書いてみただけなので、正規言語になるのは当然と言えば当然ですね。

といっても、「連立方程式、というかその係数行列として見てみる」という視点の換え方はやはり重要で、 Strassen乗算に似た（似てないかも）雰囲気の4分割再帰で行列のベキ乗和の極限つまり * を求めることで正規表現に変換、だとか、色々と面白い扱い方が考えられています。

あ、そうそう。「文脈自由言語」は、この言い方で言うと、一次方程式に限らず連立多項式の解、ということになります。

文献： [Conway 71] "Regular Algebra and Finite Machines" (もっと前の文献があるかも)

23:00 10/12/15

inplace_merge を読んでみた

C++ Advent Calendar 参加記事です。初めましての方は初めまして。

今日は、<algorithm> ヘッダの関数の中で、「今すぐ実装しろ10分以内に！！！」と言われたらすごく困る選手権第一位の

template<class BidirectionalIterator>
   void inplace_merge(BidirectionalIterator first,
                      BidirectionalIterator middle,
                      BidirectionalIterator last);

のソースを読んで、10秒以内に実装しろと言われても困らないようになりたいと思います。

あ、ちなみに何をする関数かというと、こういう、ソートされた区間が２つ並んでるときに、まとめて１個のソート区間にしてくれる関数です。

#include <algorithm>

int main() {
   int xs[] = {1,4,5,  2,3,6};
   std::inplace_merge(xs+0, xs+3, xs+6);
      // 1, 2, 3, 4, 5, 6 になる
}

いわゆる「マージソート」の途中のステップをやってくれる関数ですね。

これ、メモリを動的に確保してよいなら、 (1) last-first と同じサイズのバッファを確保 (2) そこに小さい順に書き並べる (3) first--last に書き戻す、などなど、もっと効率のいいやり方があるかもしれませんが、まあとにかく簡単です。では、余計なメモリを使えない場合は？

8 Complexity: ... If no additional memory is available, an algorithm with complexity N log(N) may be used

その場合はそれなりのやり方ってものがあるぜ、と規格に書いてありました。どうやるんでしょうか。アルゴリズムの書籍を読めばちゃんと解説が書いてあるような気がしますが、せっかくなので、手元にあった g++ 4.4.0 のライブラリのソースを読んで理解してみたい。

template<class BidirectionalIterator>
   void inplace_merge(BidirectionalIterator __first,
                      BidirectionalIterator __middle,
                      BidirectionalIterator __last)
   {
       ...
       _DistanceType __len1 = std::distance(__first, __middle);
       _DistanceType __len2 = std::distance(__middle, __last);
       ...
       std::__merge_without_buffer(__first, __middle, __last, __len1, __len2);
   }

左右の区間の長さを計算してから、追加のメモリを使えなかった場合の分岐では、 __merge_without_buffer という関数へ。

template<...>
   void __merge_without_buffer(__first, __middle, __last, __len1, __len2)
   {
       if (__len1 == 0 || __len2 == 0)
           return;
       if (__len1 + __len2 == 2)
       {
           if (*__middle < *__first)
              std::iter_swap(__first, __middle);
           return;
       }

       ...(続く)...

まず長さが極端に短いケース。左右どっちかの長さが 0 なら何もしなくていいし、長さ２なら、順番逆の時に swap するだけ。

ここからが本番。

      _BidirectionalIterator __first_cut = __first;
      _BidirectionalIterator __second_cut = __middle;
      _Distance __len11 = 0;
      _Distance __len22 = 0;
      if (__len1 > __len2)
      {
          __len11 = __len1 / 2;
          std::advance(__first_cut, __len11);
          __second_cut = std::lower_bound(__middle, __last, *__first_cut);
          __len22 = std::distance(__middle, __second_cut);
      }
      ...(まだ続く)...

左の方が長い場合、__first_cut が __first + __len1 / 2 を指すように、つまり要は左側を半分に分ける

◆◆◆◆◆◆◆◆☆☆☆☆

　　　　　↓↓↓↓↓

◇◇◇◇◆◆◆◆☆☆☆☆

で、右側は、std::lower_bound だから、つまり２分探索して、「*__first_cut より小さい部分」と「*__first_cut 以上の部分」

◇◇◇◇◆◆◆◆☆☆☆★

に分ける。こうすると、◇と☆に小さい値が入ってて、◆と★に大きい値が入ってる。なんだか◆☆の部分をreverseすると綺麗になりそう？

      else
      {
         __len22 = __len2 / 2;
         std::advance(__second_cut, __len22);
         __first_cut = std::upper_bound(__first, __middle, *__second_cut);
         __len11 = std::distance(__first, __first_cut);
      }
      ...(まだ続く)...

右の方が長い場合は、左右逆転。 ◇と☆に小さい値が入ってて、◆と★に大きい値が入ってる。こっちは upper_bound だから、「*__second_cut 以下の部分」と「*__second_cut より大きい部分」に分けるわけですね。

◇◇◇◆☆☆☆★★★

こんな感じ？この時も、◇と☆に小さい値が入ってて、◆と★に大きい値が入ってる、のは同じ。

「以上/以下/より大きい/より小さい」、をちゃんと整理した方がいいかな。

最初の lowed_bound の場合は、「☆ の最大＜ ◆ の最小 ≦ ★の最小」になるようにしてる。
upper_bound の場合は、「◇の最大 ≦ ★ の最小＜ ◆の最小」になるようにしてる。

これを踏まえて

      std::rotate(__first_cut, __middle, __second_cut);
      ...(まだ続く)...

あ、reverse じゃなくて rotate でした。ソート済み同士をマージする処理なんだから、順番逆向きにしちゃダメですよね。そりゃそうだ。

rotate は 1,2,3 | 4 を 4 | 1,2,3 に変えるようなクルッと回す処理なので

◇◇◇☆☆☆◆★★★

こうなって、どっちにせよ「☆の最大＜◆の最小」なので、☆と◆はこの順に並ぶしかあり得いので、この白と黒の切れ目は確定。あとは再帰で左 ◇◇◇☆☆☆ と右 ◆★★★ をそれぞれマージ！

      _BidirectionalIterator __new_middle = __first_cut;
      std::advance(__new_middle, std::distance(__middle, __second_cut));
      std::__merge_without_buffer(__first, __first_cut, __new_middle,
				  __len11, __len22);
      std::__merge_without_buffer(__new_middle, __second_cut, __last,
				  __len1 - __len11, __len2 - __len22);
   }

完成！

計算量は、毎回「長い側を真っ二つ」にしているので、一番バランス悪い時でも１：３に再帰呼び出しがわかれるから、 O( log_(4/3) N ) 段の再帰呼び出しで済みそう。 lower_bound と upper_bound を注意深く使っているのは、同順位の要素については並び順を変えない、安定ソートになるようにするためかな。ふむふむ。

これで皆様も inplace_merge マスターですね。明日から使いまくりましょう！

23:00 10/12/14

正規表現しちへんげ！　第十一夜

NFA は、オートマトンに文字列を読ませた時に辿れる道が複数あって、仮に path1 か path2 か (中略) か pathN という道があるのなら、その最後の状態が F に属しているものがあれば…つまり pathX.last を pathX の最後の状態とすると、「path1.last∈F OR path2.last∈F OR (中略) OR pathN.last∈F」ならば言語に入るとみなす、という定義でした。OR です。

NFA の認識する言語の定義を
path1.last∈F XOR path2.last∈F XOR (中略) XOR pathN.last∈F と変えた場合も正規言語

OR じゃなくて XOR にしてみました。NXA (Nondeterministic Xor Automaton) という呼び名がついていたりします。

元々が決定性の DFA なら、行き着く先は一つしかないので、NFA でも NXA でも結果は変わりません。というわけで、NXA は DFA よりは表現力があるので、正規言語を全て表現できます。逆に NXA も NFA→DFA と同じようなやり方で決定性にできるので、実は結局表現力は同じです。正規言語以外は作れません。

応用

初めて聞いたときは、その発想はなかったわ、と本気で思いました。なんでまだ XOR にしてみようなんて思ったんでしょうか。これはまず、DFA に比べると、NFA や NXA は巧く作れば「サイズが小さい」ということがわかっています。最も差が開く場合は指数関数的にサイズが違う。というわけで、メモリ食わないコンパクトな表現の一つとして考えられた模様です。

ところが、オートマトンのサイズを最小化するというのは難しい。「DFA の範囲で最小化」なら効率のいいアルゴリズムが幾つか知られているんですが、 NFA だと、PSPACE完全という大変な計算量の問題になってしまうらしい。ところが、 NXA なら、多項式時間で最小サイズのものが求まるのだー！という面白い性質があるそうです。不思議ですね。

文献： [van Zijl 97] "Generalized Nondeterminism and the Succinct Representation of Regular Languages"

21:00 10/12/13

正規表現しちへんげ！　第十夜

趣向を変えて、文字列じゃなくてツリーに関する正規言語、と話を拡張するとどうなるでしょうか。たとえば XML スキーマの RelaxNG などに、正規ツリー言語が使われています。

Rational Language、有限モノイド、Myhill-Nerodeの同値類、は、文字列結合演算をツリーのノードにツリーを継ぎ足す演算に一般化すると正規木言語と呼ばれているものを表します。
MSO論理式 も、文字列のインデックスの整数をツリーノードへのポインタ、大小関係を子孫関係と兄弟関係の比較、と一般化すると同じく正規木言語を表現するようになります。
NFA、DFAの一般化のしかたは幾つかあって
ツリーをルートから葉まで上から下に分岐のたびに分身しながら降りていくトップダウンオートマトン (TDA) では、 NTDA は正規木言語を表しますが、DTDA は表現力はもっと弱いです。
逆に葉からルートに向かって下から上に収束していくボトムアップオートマトン(BUA)では、 NBUA も DBUA も正規木言語を表します
分身しないで、ツリーの上を親に行ったり子に行ったりうろうろしながら判定するツリーウォーキングオートマトン (TWA) だと、NTWA も DTWA も正規木言語まで行けません。表現力弱いです。
右線形文法 を木文法に拡張すると葉にだけ非終端記号が来るもので、これは正規木言語を表現します。
左線形文法 の一般化は木文法でルートにだけ非終端記号が来るようにしたもので、これは余正規木言語、という正規木言語とは違う、なにか不思議なものを表現します。

明日はまた文字列の話に戻ります。

文献： [Thatcher&Wright 68] "Generalized Finite Automata Theory with an Application to a Decision Problem of Second-Order Logic" (有料)
文献： [Brainerd 69] "Tree Generating Regular Systems" (有料)
文献： [Arnold & Dauchet 76] "Un Théorème de Duplication pour les Forêts Algébriques" (有料)
文献： [Bojańczyk & Colcombet 05] "Tree-Walking Automata Do Not Recognize All Regular Languages"
文献： [TATA] "Tree Automata Techniques and Applications"

18:00 10/12/11

正規表現しちへんげ！　第八夜

しちへんげなのに八個以上あるのは何故？という屁理屈をそういえば何も考えていなかった。

空間計算量 o(log log N) で判定できる言語＝正規言語

DSPACE( o(log log N) ) と書きます。この小文字の o 記法はあまり見慣れないかも知れませんが、要は、入力文字列長 N に対して「log (log N)」よりも真に小さいオーダの空間しか使わないで判定できるなら、正規言語。

第六夜の DSPACE( O(1) )、つまりメモリを定数オーダしか使わないで判定できる言語＝正規言語、と合わせると、なかなかこれは面白い結果です。今まで挙げたなかで自分が一番驚いたのはこれかもしれません。メモリを本当にほんのちょびっと、ちょびっとだけ例えば O(log log log log log N) くらい使わないと判定できない、定数メモリ消費では無理だけど本当にちょっと余分に動的確保できれば…、という微妙な言語は存在しない、と言っています。定数で無理なら正規言語ではなく、その時はメモリは最低 log log N に比例する量は必要。

感覚的には、o(log log N) というのは、NFA のところに出てきた Pumping Lemma を成り立たせるには十分なくらい少量、ということです。全く同じ状態で違う位置の文字を読むことがある。というのは、メモリを o(log log N) しか使わないので、計算中に起こりうる全メモリ状態の総パターン数は、指数オーダで o(log N)。読み取り位置を行ったり戻ったりして複数回通るとしても、そのパターン数は更に指数で o(N)。文字列の長さより短い。てことで、完全に同じ状態で読まれている入力箇所が複数あるので、そこを縮めちゃってもこのマシンには区別がつかない。ので、そういう部分を縮めて実際は入力はもっと短かったのだー！！とやっても同じだけメモリを食う計算をしちゃうわけなので、実は log log N 以上のオーダであったことが判明してしまう。

みたいな論法。

文献： [Stearns&Hartmanis&Lewis II 65] "Hierarchies of Memory Limited Computations" (有料)

21:36 10/12/10

⇒ 侵略！以下娘 <=

operator<=を「オペレーター以下」と読もうとしたら「<=」がイカのAAに見えてきた

─ @tomerun

正規表現しちへんげ！の途中ですが、このページは Functional Ikamusume Advent Calendar に侵略されたんじゃなイカ？

そんなわけで、関数型イカ娘の私

<=

が地上の関数を全員征服するでゲソ。今日は手始めに、ブール関数どもを手下にして侵略の拠点としようじゃなイカ。否定（NOT）・論理和（OR）・論理積（AND）・含意（⇒）などが相手でゲソ。

では早速、Haskell を立ちあげて「論理和 (OR)」を攻略するでゲソ。おまえの動きは全て見切っているでゲソ！

> ghci
Prelude> let (<=||) x y  =  (x <= y) <= y
Prelude> [True <=|| True,  True <=|| False,  False <=|| True,   False <=|| False]
[True,True,True,False]

ちょろいもんじゃなイカ。ちなみにこんなテストは cabal install 'QuickCheck >= 2' して

Prelude> import Test.QuickCheck
Prelude Test.QuickCheck> quickCheck $ \x y -> (x <=|| y) == (x || y)
+++ OK, passed 100 tests.

自動化すると良いんじゃなイカ。

次は「否定 (NOT)」の番でゲソ。M78 星雲の宇宙人 0/0 と手を組むでジュワ。しかしこのAAはちょっと無理がなイカ…？

...> let ultra    =  0/0 <= 0/0
...> let (<=!) x  =  x <= ultra

...> quickCheck $ \x -> ((<=!) x) == (not x)
+++ OK, passed 100 tests.

これで NOT も私の配下でゲソ。さらに「論理積 (AND)」をやっつけてやろうじゃなイカ。

...> let (<=&&) x y  =  (x <= (y <= ultra)) <= ultra

...> quickCheck $ \x y -> (x <=&& y) == (x && y)
+++ OK, passed 100 tests.

最後に「含意（ならば、⇒）」を倒すでゲソ。 "True ならば False" だけが False で、ほかは True になる極悪な演算子でゲソ。そう例えばこんな

...> [True <= True,  True <= False,  False <= True,  False <= False]
[True, False, True, True]

って私じゃなイカ！！

19:00 10/12/09

正規表現しちへんげ！　第七夜

七まで来ました！でももうちっとだけ続くんじゃ。クリスマスまでは…無理かな…。

s ≡_L t　「文字列集合 L から見ると文字列 s と t は似たような物」という関係を、以下で定義する。
どんな文字列 u をとってきても、su と tu は、両方 L に入るか、両方とも L に入らないか、どっちか。
という同値関係で文字列を分類したら有限種類に分類できる＝ L は正規言語

Myhill-Nerode の定理と名前がついています。

たとえば、「a をピッタリ2回含む」文字列の集合 L は、正規言語です。この L から見ると、a を１文字も含まない人達

bbbbbb ≡_L ccccccc ≡_L 空文字列 ≡_L bbcbcbcbcbcbcb

は、どれも大差ないです。a をピッタリ2文字含む文字列を後ろに繋げたらどれも L に入りますし、それ以外の文字列を繋げたら L に入りません。区別がつかない。同様に、a を 1 文字だけ含む人達

a ≡_L abc ≡_L bca ≡_L bbaccbcbcbc

も L さんから見ると同じに見えます。同じく、a をピッタリ 2 文字含む人達、も。そして、a を3文字以上含む人達、も区別がつきません。何をくっつけてももう L に入らなくなってしまっているので。

というわけで、「a をピッタリ2回含む」視点で見ると、世界には文字列は 4 通りしかありません。有限種類です。そんなわけで、この言語は正規言語です。

応用など

まず、この定理が念頭にあると、DFA（第四夜）の「状態」とは一体なんなのか、どういう意味があるのか、ただの●と→じゃなかったのか、という感覚がわかるようになります。「この Myhill-Nerode の定理の視点で文字列を分類したら、有限通りのどれに分類されるか」を表すのが DFA（正確には最小状態数DFA）の状態。

最初は、「空文字列と区別がつかない」人達の仲間状態からスタート。例えば a を読み込んで状態を移ると、「"a"と区別がつかない人達」に分類が移る。ここで例えば a* のような正規言語だったら空文字列とaは区別がつかないので、最適化されたDFAなら、文字aを読み込むと初期状態に戻るサイクルができてるはずです。そんなこんなで、「空文字列をくっつけたらLに入る人達」状態にたどりついたら、そこはDFAのゴール状態。F。それぞれの状態は、「L からみると区別できない文字列の集合 (同値類)」を表していたのです。

エイプリルフールに書いた正規表現を微分する話もこれに関連していて、正規表現を "微分" すると有限パターンしか出てこないし、微分しまくるとDFAが作れる、というのは、裏側には、この「L からみると区別できないよ分類」があるからこそです。

左からも右からも (※2011/12/25 追記)

上では、「su と tu」のように後ろに他の文字列をいくら繋げても区別がつかない、という基準で文字列を分類しましたが、「前に繋げても区別がつかない」や「前後に繋げても区別がつかない」で分類しても、やはり正規言語なら有限通りになりますし、逆に有限通りなら正規言語です。後ろに繋げて区別するのが最小DFAに直接対応するわけですが、前後繋げによる区別はモノイドに対応します。

文献： [Nerode 58] "Linear automaton transformations" (有料)

20:00 10/12/08

正規表現しちへんげ！　第六夜

偶数夜はオートマトン方向から攻めるシリーズにしようかどうしようか。今夜はシンプルです。

空間計算量 O(1) で判定できる言語＝正規言語

DSPACE(1) と書きます。非決定性チューリングマシンでも同じ事が言えるので、NSPACE(1) でもある。

入力文字列が条件にマッチするかどうかの判定ルーチンを「再帰でスタックも使わず、動的なメモリ割り当てもせず、入力は読み取りだけで書き換えもせず」ループと条件分岐だけで作れたらそれは正規言語です。正規言語でなければ、判定に必ず再帰か動的なメモリ確保が必要です。プログラマ的には、これが一番わかりやすい定式化じゃないでしょうか。

ちょっと待って、と思うかも知れません。

bool is_paren_match(const char* input) {
  int paren = 0;
  for(; *input; ++input) {
    if( *input == '(' ) ++paren;
    else if( *input == ')' ) --paren;
    if( paren < 0 ) return false;
  }
  return paren==0;
}

これは有名な「正規言語じゃない」言語、「括弧の対応がとれてる」を判定できちゃってますが…と思いきや、そうでもありません。このコードでは、intが32bitなら、せいぜい4294967295段ネストくらいまでの括弧しか判定できないので、これでは完璧じゃない。（メモリやスタックが無限にあると仮定して）完璧を期すならスタックを組むか BigInt 的なもので動的にメモリ割り当てするかになってしまいます。なのでやっぱり「括弧の対応がとれてる言語」は、正規言語ではない。逆に言うと、上のように定数メモリで書けてるので「4294967295段ネスト以内で括弧の対応取れてる言語」は正規言語です。他には、例えば昨日の例にあった「a の後に必ず b」言語などは、bool のフラグ１個持っておけば判定できるので、正規言語とわかります。

別の意味で、ちょっと待って、と思うかも知れません。これって第四夜の「DFA で判定できる」と同じ事を言ってない？

実際、かなり近いです。DFA の「状態数が有限」というのは、要するに、メモリ使用量が定数、動的割り当てをしない、というのと同じ事を意味しています。違いは、DFAは、入力を左から右に一直線に読み取ることしか許されませんが、こちらの定義では、後ろに戻って読み直したりしてもいいですよ、というところ。（と言っても、ポインタを保存しておいて…等々やってしまうと log(文字列長) の記憶領域が必要なので、 --input でチマチマ戻るくらいのことしかできませんが…。） DFA よりは強力なことを言ってます。

でも、この違いは実は表現力を変えない、行ったり戻ったりすれば（定数メモリ消費で）判定できる条件なら、必ず左から右に１パスでも判定できる、ということがわかっています。

文献： [Shepherdson 59] "The Reduction of Two-Way Automata To One-Way Automata" (有料)
文献： [Rabin&Scott 59] "Finite Automata and Their Decision Problems" (PDF)

22:30 10/12/07

正規表現しちへんげ！　第五夜

正規言語の定義を並べるシリーズ。定義というか、なんでしょう、「特徴づけ」でしょうか。

今日は、マッチする文字列に関する条件文を、論理式で書きます。

～ && ～　（意味：and）
～ || ～　（意味：or）
　! ～　（意味：not）
∀x : num ～ （意味：0以上文字列長未満の全ての自然数 x について、～が成り立つ）
∃x : num ～ （意味：0以上文字列長未満のある自然数 x について、～が成り立つ）
∀X : set ～ （意味：全ての、0以上文字列長未満の自然数の集合 X について、～が成り立つ）
∃X : set ～ （意味：ある、0以上文字列長未満の自然数の集合 X について、～が成り立つ）
is_a(E) （意味： E 文字目が 'a'）
is_b(E) （意味： E 文字目が 'b'）
...　（以下すべての文字について is_?(E) が使える）
E<E, E<E, E==E, E!=E, E>E, E>=E （意味：自然数の大小比較）
E ∈ X （意味：自然数 E が集合 X に入っている）
式 E には、num型の変数か、E + 定数 か、文字列の長さを表す特殊定数 $ が書けます。
という形の論理式で条件を書ける場合だけが、正規言語

この定義を、「MSO-Definable Language」と言ったりします。MSO = Monadic Second-Order logic。

たとえば、∀x:num (!is_a(x) || ∃y:num (x<y && is_b(y))) と書くと、文字 a が出てきたら、その後ろには必ずどこかに b が出る、という条件を表します。これを満たす文字列の集合は、正規言語です。正規表現で書くとどうなるかな。 [^a]*(a.*b[^a]*)* かな。

使える論理式は、C言語なんかのブール式に比べると、∀ (forall) や ∃ (exists) がある文、強力です。でも逆に、変数同士の足し算がなかったり、for や while ループで計算した結果を利用して…などができないところは、表現力が制限されてもいます。この定義は要するに、「自然数と集合に関する∀と∃という強力な式さえあれば、式一発で書けちゃうくらいの条件」というのが正規言語の定義、と言っています。

応用

NFAやモノイドは正規表現の実装に使える、という話でしたが、今回は、どちらかというと逆ですね。「MSO論理式の真偽判定の実装に、正規表現（と同値であるという性質）が使える。」

forall や exists を大量に含むような複雑な論理式、無邪気に毎回全部の自然数/集合を調べてチェックしていたら、時間がかかり過ぎてしまいます。ところが、このMSO論理式は実は必ず正規表現と等価ということがわかっているので、頑張るとDFAなどにコンパイルできて、どんな複雑な式でもループ１発で判定できてしまいます。こういう効率的な論理式チェックに有効なのです。

正規言語は、「文字列の検索や置換」だけでなく、「状態遷移システムの仕様」や「イベント発生列」のパターン記述にも使われます。そもそも、正規表現の初出は "Representation of Events in Nerve Nets and Finite Automata" [Kleene 56] という、神経網の活動の記述手段を考える、という論文らしい。（※追記 "A Logical Calculus of the Ideas Immanent in Nervous Activity" [McCulloch & Pitts 43] まで行ける、と成瀬さんに情報いただきました。ありがとうございます。）コンピュータ寄りの話にしてみると、ファイルを触るときは open (read|write)* close 以外のパターンで触ってはいけません！などという使い方。このくらいの条件なら簡単に正規表現が思い浮かびますが、もっと複雑なシステムの複雑な仕様だとそうでもないので、論理式で書いて、その検証にDFAやなにかを経由したりします。

文献： [Büchi 59] "Weak Second-Order Arithmetic and Finite Automata"

17:35 10/12/06

正規表現しちへんげ！　第四夜

また定番を片付けに戻ります。文字集合を Σ とする。

Q = "状態"の有限集合
E = Q×Σ から Q への関数
i = Q の要素一つ
F = Q の部分集合
が存在して、状態 i から F に属する状態まで、E に属する道をたどって歩いて作れる文字列
という形で表せるものが正規言語

正規言語の第四の定義は、「DFA (Deterministic Finite Automaton) で受理できる言語」。

第二夜と何が違うかというと、E と i だけが違います。Q×(Σ∪{""})×Q ではなく関数になったので、今の状態と文字が決まると、次の状態は一つに決まります。また、スタートが集合ではなく一要素になったので、どこから始めるかも一つに決まります。そういう意味で Deterministic。行き先は常に一つ！

DFA の方が実行する時の効率は NFA よりよいので、これも実装に使われます。ただし、拡張正規表現を扱うのが NFA の方が簡単なのと、NFA を DFA にするとサイズが爆発する可能性があるので、 NFA のまま動かす、という方がメジャーですね。

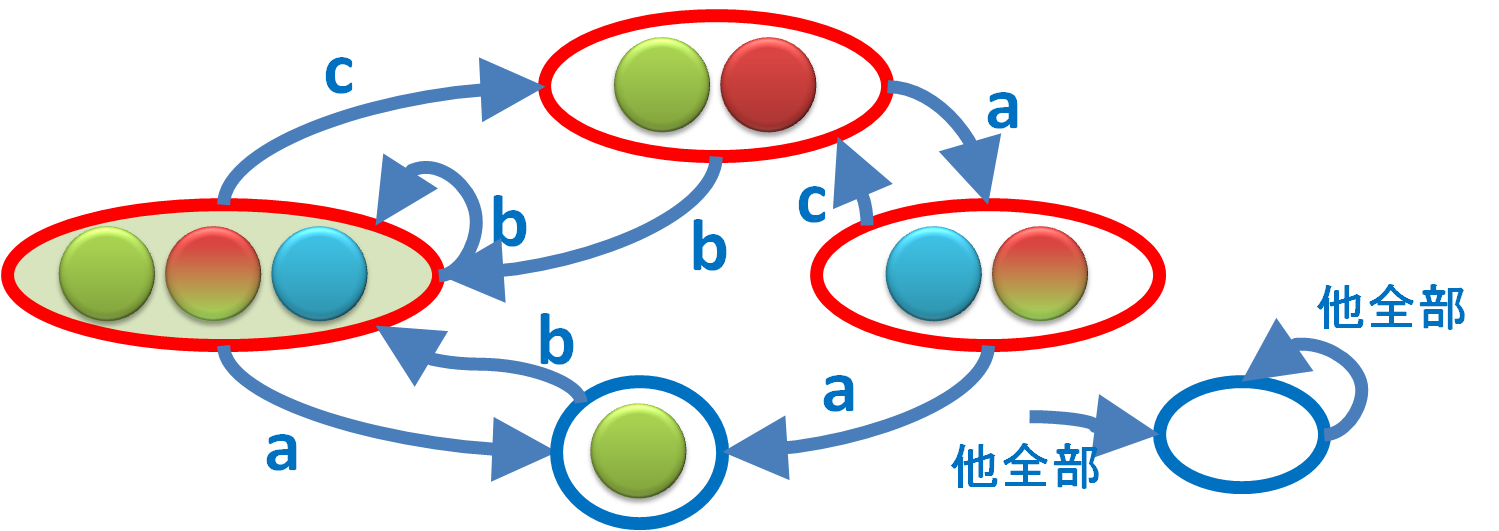
Deterministic は Nondeterministic の特別な一例なので、「DFAで受理できる」は「NFAで受理できる」よりも弱いように思えます。けど、実は一緒だよ、つまりNFAは全部DFAに変換できるよ、というのが面白いところ。

NFA から DFA への変換は、「NFA の状態の集合の集合」を「DFA の状態の集合」と見なす、という何か怪しげな変換でできます。「Powerset Construction」と呼んだり「Subset Construction」と呼んだり。 DFA の状態はNFA状態の集合なので、{●, ○, △} みたいな形をしています。これは「NFAでIから走り始めると●か○か△にたどりつきます」という状態を表してます。「●か○か△にいる状態」で文字 a を読むと「□か◆」に着くなら、{●, ○, △} から {□, ◆} に矢印を引きます。そんな感じで適当に矢印を引いていくと、「●か○か△にいます」と常に可能性を全列挙するので、その全列挙の可能性は一つしかない、つまり Deterministic になります。（上の図は第二夜の例をDFA化してみたつもりだけど間違ってるかも。）

「NFA と DFA が等価」というは当たり前でないようで当たり前なようで、やっぱり当たり前でない話です。 Deterministic な計算と Nondeterministic な計算の表現力が同じかどうか？という問題は、有名な「P =? NP」問題も同じ雰囲気の構造を持っていて、そちらは多分等しくないだろうと予想されているわけですし。 (N|D)FA を拡張したプッシュダウンオートマトン (N|D)PDA では等しくないことが証明されていたりします。不思議ですね。

文献： [Kleene 56] "Representation of Events in Nerve Nets and Finite Automata"

22:04 10/12/05

正規表現しちへんげ！　第三夜

はい、なんだかよく分からないと思うので、ちょっとだけ用語の準備をします。集合 M と、結合則 (x op y) op z = x op (y op z) を満たす演算 op :: M×M→M と、単位元 e (e op x = x, x op e = x を満たす) があるとき、 (M,op,e) をモノイド (monoid)と言います。

モノイド

　・ (自然数, +, 0) はモノイドです。(a+b)+c=a+(b+c) で、a+0=0+a=a なので。
　・掛け算 (自然数, *, 1) もモノイドです。(a*b)*c=a*(b*c) で、a*1=1*a=a なので。
　・ (文字列, 文字列結合, 空文字列) もモノイド。文字列結合を~と書くことにすると、 (a~b)~c=a~(b~c) なので。
　・偶＋偶＝偶、偶＋奇＝奇、奇＋偶＝奇、奇＋奇＝偶とすると、({偶,奇}, ＋, 偶) もモノイドです。

まあ、結合則を満たして、あとは、0 みたいな、演算しても値を変えないものが居れば、だいたいなんでもいいです。名前をつけた方が格好いいでしょくらいの感覚です。一つだけ重要なのは、3つ目の、文字列は文字列結合演算を考えると、モノイド。

あ、もう一つ重要な話がありました。上の4つ目の例は、{偶,奇} の2個しか値がないのです。他は自然数や文字列なので、無限に種類があるのですが。{偶,奇} のような有限種類の値しかないモノイドを 有限モノイド (finite monoid) と呼びます。

準同型

もう一つ準備。モノイド (M1, op1, e1) からモノイド (M2, op2, e2) への関数 f のうち
　　f(e1) = e2
　　f(x op1 y) = f(x) op2 f(y)
を満たす物をモノイドの 準同型写像 (homomorphism) といいます、なにか難しいですが、今回 M1 としては文字列だけ考えるので、文字列限定で考えましょうか。「文字列を、適当に真ん中でぶった切って別々に計算してからまとめる」という計算ができる ⇒ 準同型。

たとえば、文字列の長さを計算する length 関数は、準同型です。
　　sを適当にs=x~y (~は文字列結合) になるようにぶった切って、 length(x) と length(y) を計算して足す、と length(s) が求まるので。
「適当に」が重要で、ここでどういう切り方をしても結果は同じ。そういうのが準同型なのです。

もう一個、文字列から空白を取り除く rmsp(x) = x.gsub(/\s/,"") 関数は、準同型。
　　sを適当にs=x~y になるようにぶった切って、rmsp(x) と rmsp(y) を計算して結合
でもrmsp(s)と同じ結果になりますから。

はい、準備完了。

定義

有限モノイド (M,op,e)
M の部分集合 F
準同型 g :: string → M
gするとFに入る文字列の集合 {x | g(x)∈F} は正規言語。正規言語はすべてこの形で書ける。

この定義を「Recognizable Language」ということがあります。

応用

オートマトンでは左から順に文字列を読んでいかないと判定できませんが、モノイドなら「文字列をぴったり真ん中で割って左右両方で計算して、あとでまとめる」ができます。スレッドが100個あったら、100等分して並列に計算してから最後にまとめ、とできます。というわけで、有限モノイドは、長い文字列に対する正規表現パターンマッチの並列化が可能な表現です。（※ 実際には有限モノイド表現のサイズはかなり大きくなってしまって効率が悪いので、特殊な条件を仮定してこの使い方をすることが多いようです。）

なんとなくの説明

たとえば、「長さが偶数の文字列」は正規言語です。M を最初の例4の {偶,奇} モノイド、F を {偶} として下さい。こんな風に、{偶,奇} のように 「文字列を有限パターンに分類」 することで分割して判定できるのが正規言語、というわけです。全ての正規言語がこの形で書ける証明は、まず正規言語をNFAで表現してから、文字列を「この状態からスタートしてその文字列を読み込んだらどの状態に行けるか」という、状態×状態の対応表でパターン分類してやればよいです。NFAの状態数は有限なので、対応表のサイズも有限。

応用２

私もちょっと前に知って面白いなーと思った話で、 Factorization Forest というのがあります。

文字列を２分割、２分割、２分割…としていくと、文字列長 N なら、バランスよく分割すれば高さ O(log N) の木になります。ここで追加のオプションとして、固定の有限モノイドを一個決めて、 それで分類すると単位元 0 になる 部分文字列だけは二分木じゃなくて何個でも一気につなげて木のノードをつくってよい、としてみる。つまり、有限モノイドの元のリスト a[1] ... a[N] を、「a[i]とa[i+1]をまとめてa[i] op a[i+1]に置き換え」と「a[i]=0, a[i+1]=0, ..., a[j]=0 をまとめて 0 に置き換え」の２種類の操作を繰り返して木を作る。と、これはうまくやれば必ず定数 O(1) の高さで抑えられるそうな。この木構造は、O(木の高さ) で、任意の部分文字列が正規言語に入るかどうか判定できるインデックスとして使えるのだとか。

文献：？

21:47 10/12/04

正規表現しちへんげ！　第二夜

有名どころから片付けましょう。正規言語の定義を延々と並べるシリーズ。文字集合を Σ とする。

Q = "状態"の有限集合
E = Q×(Σ∪{""})×Q の3つ組みの部分集合
I = Q の部分集合
F = Q の部分集合
が存在して、I に属する状態から F に属する状態まで、E に属する道をたどって歩いて作れる文字列
という形で表せるものが正規言語

この (Q,E,I,F) のことを Nondeterminitic Finite Automaton (NFA) と言います。 Q が有限なので Finite で、１個の●から同じ文字の→が複数出てて行き先が一つに決定しないので Nondeterministics。正規言語の第二の定義は、「NFA で受理できる言語」です。

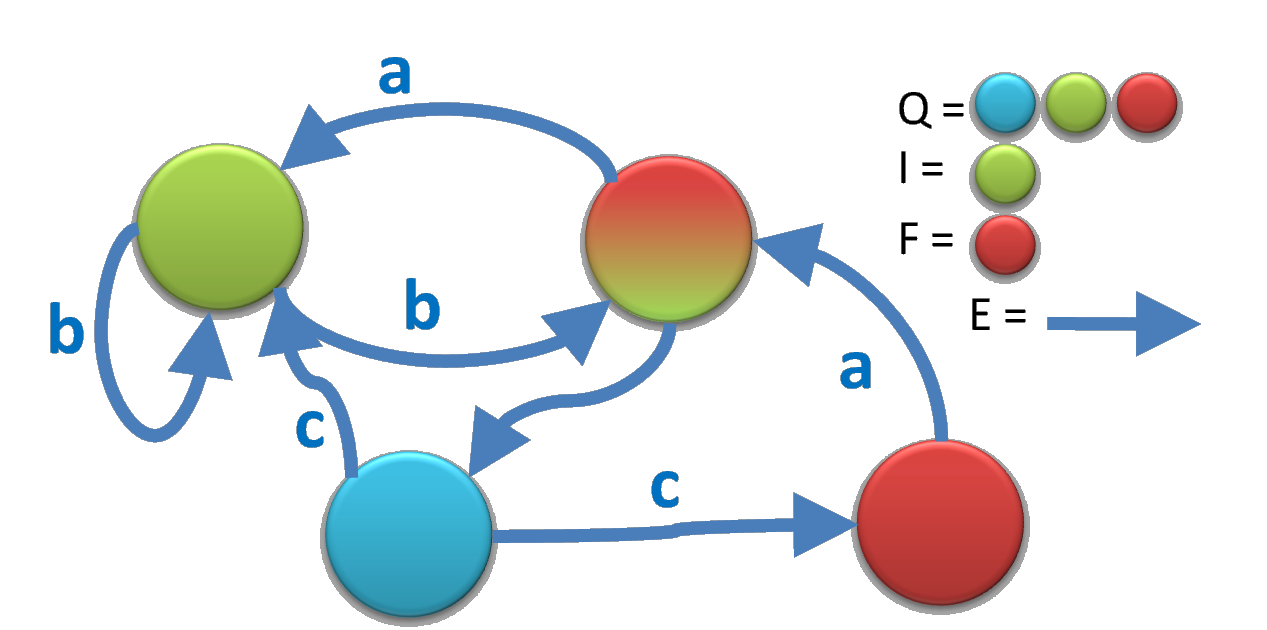
言葉で言うと何を言っているかさっぱりですが、絵で描くと上の絵のような雰囲気です。黄緑の●から赤の●まで行ける経路には、b や babbbbcac や bca などなどの文字列があるので、これらは、この NFA が表す正規言語に含まれます。逆に、ba や bcaa は入りません。こういう風に、●と→で表現できる図形で表せれば、正規言語。そうでなければ正規言語でない。

この定義は、正規表現の「実装」によく使われます。どの"状態"にいるかを整数で表して、矢印 E を状態と文字で引けるテーブルなどで表す雰囲気で、自然にマシン向けの表現になります。

もう一つ、この定義が使われるのは、ある言語が正規言語ではない、と判断する証明手段としてです。「正規言語ならば、NFAで表現できるはず」「NFA で表現できるなら、その言語に含まれる十分に長い文字列は、NFAの同じ状態を何回も何回も繰り返し通るはず」「ということはその "繰り返し" 部分の繰り返し回数を減らしたり増やしたりしても同じ言語に含まれるはず（Pumping Lemma）」「そうなっていないなら、正規言語ではない！」みたいな論法。

文献： [Rabin&Scott 59] "Finite Automata and Their Decision Problems" (PDF)

21:17 10/12/03

正規表現しちへんげ！　第一夜

正規表現（せいきひょうげん、regular expression）とは、文字列の集合を一つの文字列で表現する方法の一つである。

─ wikipedia

重要な概念には、しばしば複数の、しかし同値な定義のしかたがあります。

文字列の検索や置換をするスクリプトでよく使う正規表現、これで表せる文字列パターンのことを 正規言語 といいますが、これもそんな重要な概念の一つです。余りにたくさんの数学的な定義があるので、最近流行の Advent Calendar 風に1日1個紹介してっても、クリスマスまで持つのではないか。ということで、後先考えずに初めてみましょう。

空集合 {} は、正規言語
空文字列だけを含む集合 {""} は、正規言語
特定の一文字の文字列だけを含む集合 {"a"} や {"b"} や {"c"} や ... は、正規言語
L1 が正規言語で L2 が正規言語なら、その文字列結合 {xy | x∈L1, y∈L2} は、正規言語
L1 が正規言語で L2 が正規言語なら、その和集合 L1 ∪ L2 は、正規言語
L が正規言語なら、その0回以上の繰り返し {""} ∪ {x | x∈L} ∪ {xx | x∈L} ∪ {xxx | x∈L} ∪ ... は、正規言語
以上のやり方で作れる集合だけが、正規言語

この定義には別名がついていて、「Rational Language」とも言います。（もちろん Rational Language == Regular Language なのですが、文字列以外の色んな概念に拡張してみると、文字列では同じものを表していた定義も意味が分かれてきたりするので、一般化できる定義には別名がついてたりします。）

たぶん、この定義が一番、プログラミングで使う「正規表現」に近いですね。表現力的には、文字列連結と | と * さえあればなんとかなって、他の演算は、a+ は aa* と書けるし、a? は (空文字列)|a、 [^abc] は (d|e|...全文字並べる...) などなど、一応表すことはできるので、その一番プリミティブな演算だけを使って「定義」としています。（※ いわゆる「後方参照」は数学的な意味の正規言語の能力を超えてしまうので、今回はお引き取りいただきます）

参考資料

正規言語の理論よりの話としては、 PDF が公開されている J. Berstel, Transductions and Context-free Languages や J.-E. Pin, Mathematical Foundations of Automata Theory というテキストが勉強になりました。 Wikipedia の Regular language にも結構まとまってます。