23:06 10/06/21
ICFP-PC 2010 参加記
3日間 ICFP Programming Contest 漬けでした。 チーム名は oh!tomaton で、 tsukuno、 mayah との3人チーム。 結果は 27位 (Top 5 は非表示になってます) でした。 以下ネタバレ込みです。ご注意を。
- icfp10.zip (ソースコード一式)
- 使った言語は、Rubyで:サーバから車データ取り込み → OCamlで:chamberやtank数解析して注釈 → Rubyで:適当な難易度の問題をピックアップして解答ラインに乗せる → OCamlで:車データから焼きなまし法のソルバ(C++)を生成 → C++で:車に合う燃料見つける → OCamlで:燃料を3進ストリーム形式にエンコード → Dで:3進ストリームを回路形式に変換(終了数時間前にこの部分は "Javaで" に置き換え) → Rubyで:サーバにsubmit、でした。 あと細かいスクリプトがPHP,Ruby,バッチファイルで書かれてました。
どういう問題だったかは、 mame さんの記事 にとてもわかりやすく要約されています。
全体的に
2006年の 「関数型言語の研究&プログラミングの世界には面白いテーマや技術が転がっていて、
せっかくICFPでやるコンテストなんだから、
そういうところから面白さを取ってこれるといいね」
という方向が、
まさにそうあって欲しいとこのコンテストに期待しているところだったのですが、
今回はその意味ではパーフェクトでした。
大絶賛したい。
主催者による元ネタ解説
によると、文字列書き換え系の停止性判定問題をゲームに仕立て直しての出題なのだそうです。
いや素晴らしい。
しかし、最初の方の 「細かい仕様はguessしろ」 フェーズはやめた方が面白くなるんじゃないかなあ。 要は「2入力2出力の3進論理ゲート(どういうゲートかは書かないので頑張って当ててね)で組んだ回路を、 サンプルのような記法(文法は説明しないので推測してね)で設計して、 あるデータ構造をエンコードした3進数ストリーム (エンコード方式はサーバのエラーメッセージから推定してね) を出力するようにして送ろう!」 というのが問題の半分なんですけど、ゲート推測の部分は純粋にプログラミングの問題なのでいいとして、 他は、面白い本題への道を無駄に遠くしちゃってると思う。パズルコンテストじゃないんだから。
もひとつの不満点は、サーバの重さ。 この問題設定だとサーバへの自動化されたアクセスが殺到するのはやる前から明らかなので、 もうちょいなんとかして欲しかったかも。「この量のアクセスに対して今回程度のダウンタイムで済んだのはよくやった方」 というのはわかるのですが、そうじゃなくて、 そもそも最初からさばきれない量のアクセスが来ない問題設定にすべきじゃなかろうかと…。
Day 1
開始 0 時間後: 問題ダウンロード。読み始める。"guess" 多い…。 これ行列の不等式を満たす最適化問題に見えるけど、要するに整数計画問題かなあ。 一言で要せちゃう問題だと物足りないなあ。ううむ。 この依存関係云々の制約を使うと別種の問題になるのだろうか。 (※ あとでよく考えたら全然線形ではなくめっちゃ非線形だった…)
開始 3 時間後: とりあえずずっと回路の文法の推測をしていましたが、この辺でやっとわかった。
開始4時間30分後 (guess_gate.cpp): 次はこの 0# というゲートの演算内容の調査。
回路 0L:X0R0#X0R:0L
と 0R:0RX0#X0L:0L
と 0L:X0L0#0RX:0R
と 0R:0LX0#0LX:0R をサーバに入れてみて、
最初の17tritの出力を得る(※正確には、この時点ではなぜか先頭に0と1は来られないと勘違いしていて、
0,1は使わず2番ゲートでやってましたが)。
で、 2入力2出力の3進ゲートは高々(3*3)^(3*3)通りしか存在せず、
最初の入力ストリーム17tritもわからないけれど、 これも3^17通りしか存在しない。
あと、各ゲートの出力の初期値は…たぶん 0 だろうけど一応これも 0,1,2 の3通り調べる。
さっきの4つの出力に合う物はどれか、 適当に前の方から枝刈りしながら全探索。
幸い、1パターンしかないことがわかった。
入力ストリームの最初の 17trit と、ゲートの演算内容 (x,y)→(x-y,xy-1) が判明。
(※ X::X で入力は見られるのはこの時はまったく気づかなかった…)
開始5時間後: 回路シミュレータを書いてみる。"backward は delay 1" という問題文の定義がわからないけど… 入力Xに遠い方から近い方に戻る接続が backward かな?でも同じ距離のゲート間だと一意に定められない、 ということは、 回路グラフの構造じゃなくて、 ノード番号から forward/backward を定めるしかない。 a > b なゲートを a の出力から b の入力に繋いだ場合、1 クロック遅れるということだ。 それしか妥当な定義の仕方があり得ない。これは要は毎クロック、単にゲート番号の順に出力を更新していけばOK。 できた。サーバと結果は合う。これでTaskに載ってる回路を動かすと、"11021210112101221" という出力が得られた。次の問題は、これをサーバからの入力列で出力すること…。
開始17時間後: チームメイトはゲート数1~4の回路を全探索して欲しい出力を出す物がないか等調べていた模様。 私は、「この 0# ゲートは2進でいうNANDのような普遍ゲートになってたり… すると思うけど他の論理ゲートの組み方がわからない…」 「2入力2出力って量子ゲートっぽいな!なんかこのゲートはControlled-NOTゲートの3進バージョンになってたりしないか」 「ググったら3進制御notの論文が色々出てくる。面白いなー」 とか関係のない方向で時間を潰していました。
しかしまじめに、「欲しい出力を出す回路」ってわからないなーと思って、 何故かというと入力ストリームが勝手にどんどんやってきて、 捨てることができない上にあんまり予測できないので、出力がどんどん汚染されてしまう。 というわけで、まずは入力に非依存で出力が決まるような「入力X捨て回路」を作ってみることに。
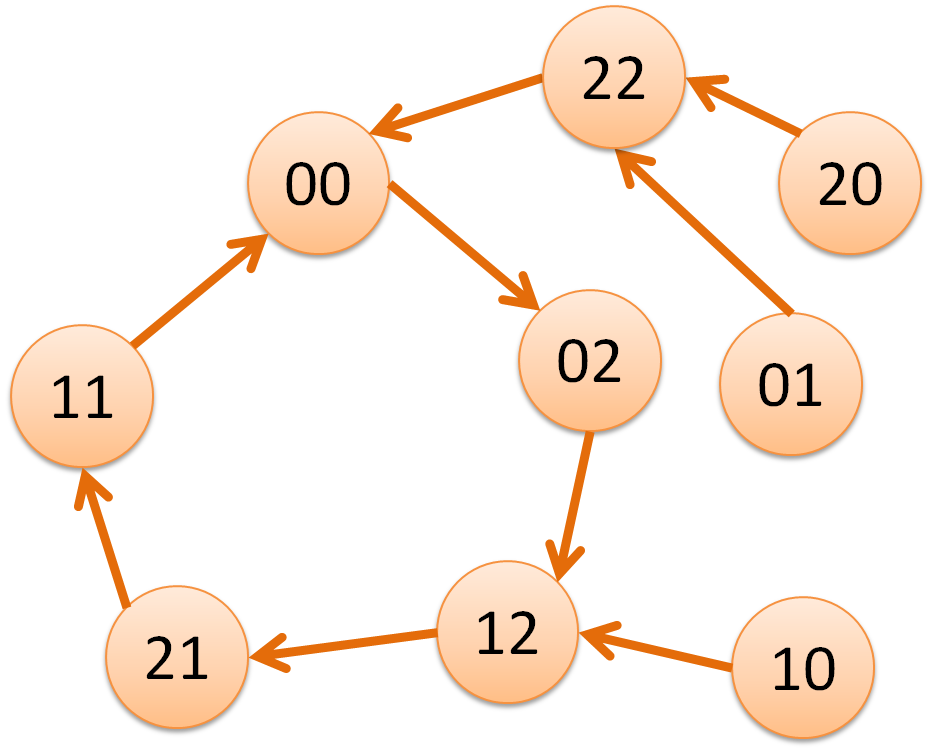
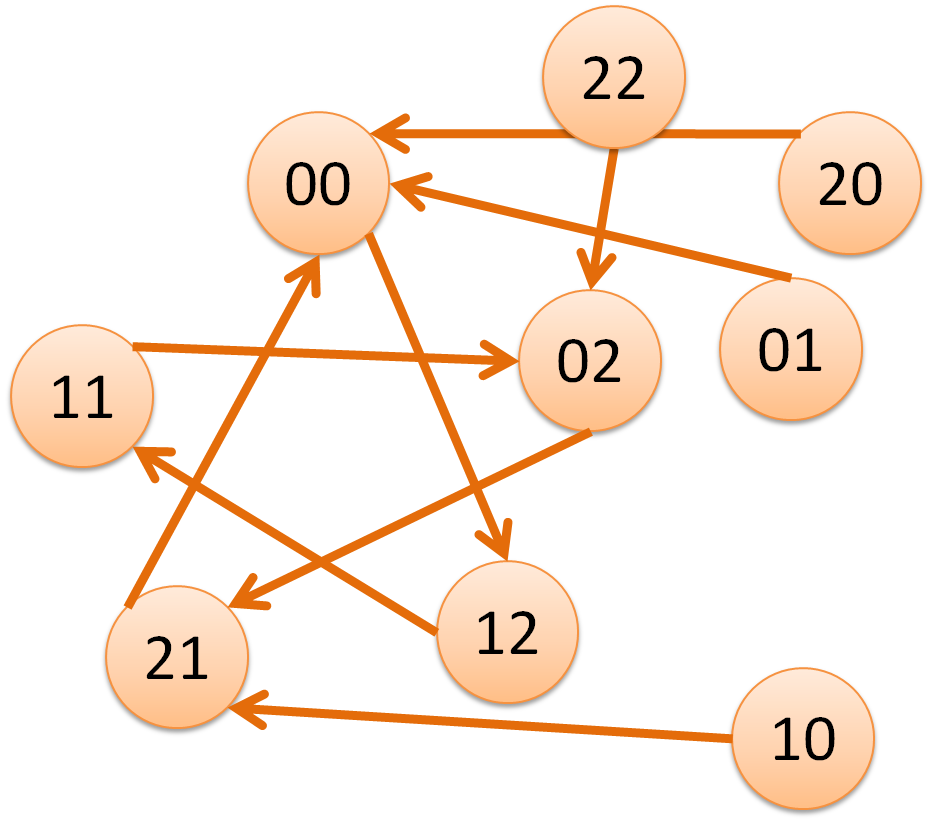
複雑な組み合わせはわからないので、ひたすら 0# ゲートを縦に繋ぎまくったらどういう状態変化をするか、 を考えると左図のステートマシンになるので…的な図を書いてひたすら。 「初期状態がなんであれ、2歩進むと真ん中のループに乗る」 「ので2歩一気に進むステート遷移を考えると右図。1歩でループに乗る。9個の可能性があったものが1歩で5個に減る。」 「02 と 12 が可能な状態な時に左右入れ替えると、20 と 21 になって次で合流して1個可能性が減る」 これを繰り返すと可能な状態は最終的に1つになって、定数出力回路が完成、という思考を経て24ゲートの、 1ばっかり出力する回路が完成。
開始20時間後 (fuel.d): 定数がなんだというのだ…依然さっぱり目的の出力を出す回路がわからない…。 ゲートをストリームからストリームへのunfold的な関数と見なし、その合成則を用いてなんたら。 …無理。
要は何が難しいかというと、 最初の1tritなら、 適当に探索すればそれが出てくる回路は見つかるんですけど、 じゃあ次の1tritを狙った物出そう、 とすると、 その分の回路を付け加えたせいで、 うまくいってたはずの最初の1tritまで壊れてしまうんですよ。 だから結局全体一気に探索しなければいけなくて無理…。 あ、
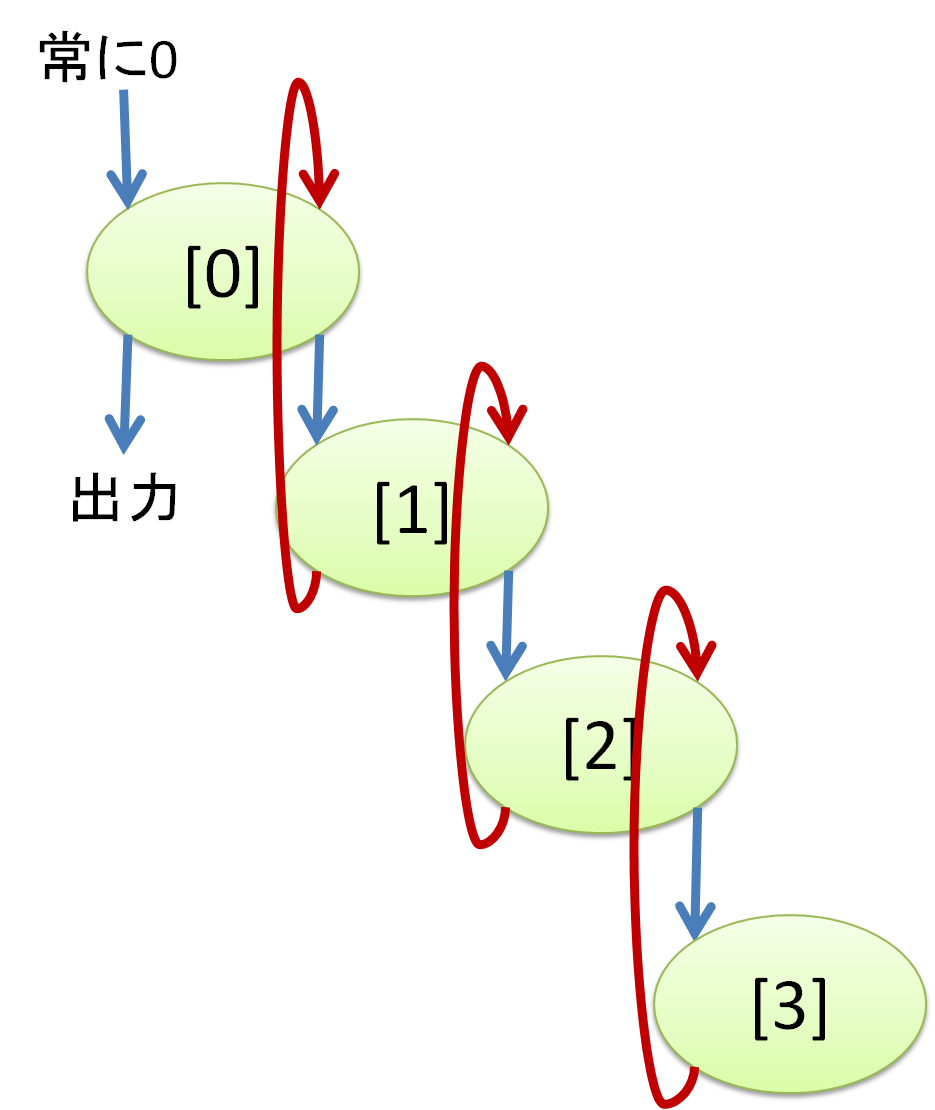
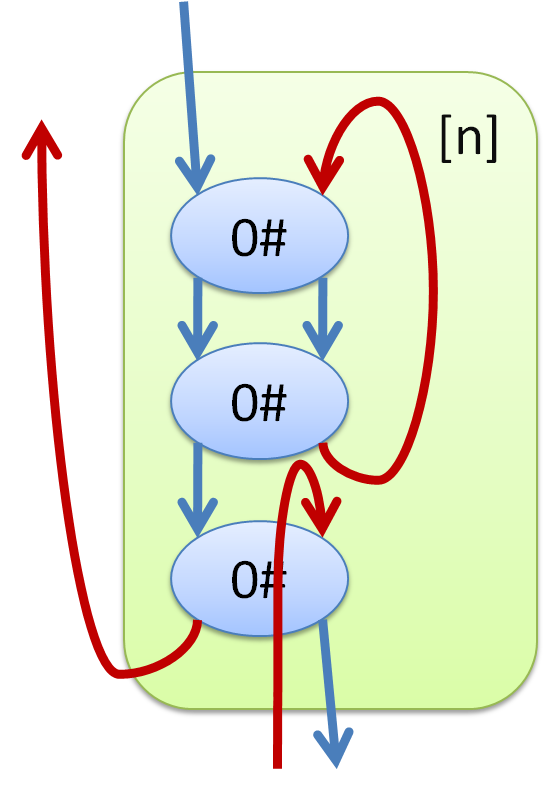
これでいいんじゃないか。左図のように繋ぐ。 [0] の中身をうまく決めて、欲しい出力の最初の 1trit を出す。 これは、右図のように 0# を縦に繋ぐ個数を増やしまくればいつかは必ず欲しい出力になるはず。 そしたら、次に [1] の中身をうまく決めて、欲しい出力の次の 1trit を出す。 [1] の中身は、1 clk 遅延があるので、どう変えようとも先頭tritには影響しないから安心して探索できる。 というのの繰り返していくらでも延ばせる。できた! (※ 先頭に固定の 24ゲート、残りは、1tritにつき実装の都合で3~5個くらいゲートを使うので平均で24+4nゲートくらい。 のちに 6+3n に改善。最終的にはtsukunoさんの1.66n に置き換え)
開始20時間30分: mayahさんとチーム合流することに。 だいたいどちらも同じような進捗であることがわかる。次なるタスクは3進ストリームのフォーマット解析…
Day 2
ライトニング部門終わってしまった。
開始25時間: 紆余曲折の末、やっと3進ストリームの読み方がわかった。
とにかくまずは
「Taskの記述からして、車データは
list<tuple<bool, list<int>, list<int>>> 型なはず」
ということを念頭に、サーバに 0, 00, ..., 01, ... 1, 10, .. と辞書順でデータを送りまくって、
パースエラーメッセージからの推測でした。
「1000 がどうも、chamber1個でtankを使わない最小の車っぽい」
「10 とだけ打つと、"次に来る数字は0か1だけ許可" と怒られるので、
ここにboolが入ってるっぽい」
「0が0で10が1っぽい」
「11000が[0],true,[]という車っぽいエラーメッセージが出る」
「111000が[1],true,[]という車っぽいエラーメッセージが出る」
等々試しているうちに、数字のフォーマットが判明 → リストは長さ・要素・要素・…の形式っぽい。
関数型なのでconsとnilと信じていたのに! → タプルは型情報決め打ちで要素が並んでいるだけか、
という流れ。
開始26時間 (tdecode.ml): mayahにより3進デコーダが書かれる。車のspecを渡すとわかりやすく表示してくれるもの。 私はさっき書いた探索アルゴリズムを実装してました。さっきは「探索」の部分は手でやっていたという…。ともかく完成。 tsukuno さんがタンク1個の車なら全部 {{{2}}} で解けるよね、と解いて、ここでやっと本題が解ける体制がスタート!
開始29時間 (tencode.ml): 3進エンコーダ。手計算で小さい車をどんどん解いていく人。 ここで TCO10 のアルゴリズム部門予選につき中断。 終わったら寝る。
開始36時間: とりあえずソルバを書かねば、 ということで乱数生成を不等式全部満たされるまで頑張るルーチンを書いてみる → 全然ダメだった。色々考えてみるけどいい案が浮かばない…。
開始38時間 (carlist.rb, submitfuel.rb): そろそろ手作業が明らかに厳しくなってきたので、サーバとのやりとりの自動化を図る。 サーバ側のWebインターフェイスを、ブラウザ経由しなくてもローカルからコマンドラインで叩けるようにしておこう。 Mechanize って名前はよく聞くけど使ったことが無かったので、 この機会に使い方覚えようかなーと。できた。現在登録されている車の一覧をとってきてテキストに落とすスクリプトと、 車IDと燃料回路を指定したらサーバにsubmitするスクリプト。
開始42時間: さっきの定数出力に24ゲート使っているのは無駄すぎるので、皆で改善案を考える。 3ゲートで00か02に絞り込む回路がtsukunoにより提案されたので、それをベースになんとか。 さっきのステートマシンを紙に書いて、チェスの駒を00と02に置いて、 進めて、時には左右swapして…と遊んでいたら思いついた。 ループ内からは左右入れ替えても01や10に飛べないので合流ポイントは00しかない。 その2clk前が20と21なら合流できる。これは左右入れ替えると02と12。これは00と02から一個進んだところ。 というわけで 0# X 0# = 0# = 0# X 0# = 0# の6歩で行ける。
開始43時間30分(annealing.cc): 結局、うまい解き方も思いつかないので、 もはや焼きなます しかない!!との結論に達し、書き始める。 "焼きなまし法 ライブラリ" でググったらトップだった nodchip さんのコードをお借りして書き始める (※ バージョンアップされたらしい)。 (左辺 - 右辺) が正ならエネルギー 0、そうでなければ絶対値が大きいほどエネルギー大きいという感じで、 行列の要素をどれか適当に選んで変える操作を近傍とする。 mayahと私で同時に書き始めたけどmayahさんの方が先にまともに動く物を完成。負けた…! 多少複雑そうなのも解けていたので、これを実践投入することに。
開始45時間30分(tauto.ml): mayah さんにより、 car の3進ストリームを読み取って解いて燃料を3進ストリームで返す流れが完成。 OCaml のインタプリタモードで、上から順に実行していく途中でOCamlのソースをファイルに吐き、 下の方で #use "そのファイル" すると動かせるという謎のeval技術が開発されていた。なんだそれ!
開始46時間30分(trial.rb): carlist.rb → tauto.ml → fuel.d → submitfuel.rb のチェインを繋ぐ。 これで放っておけば完全自動で問題を解いていく夢のシステムが完成…! 以降、これをずっと2マシンでぶん回しています。 tsukuno さんはSAでは辛そうな、答えがBigIntegerになるように作られた雰囲気の不等式を専用ルーチンで解いたりしている。
Day 3
開始53時間30分(genCar.cpp): mayahさんが焼きなまし法をひたすら改良し、 tsukunoさんは怪しげな戦略が必要そうな問題を各個撃破しているので、 することなくなった私はそろそろ車でも出荷するかと書き始め。 といっても、ランダムに行列を6個生成 → ランダムに行列掛け算式を10000個生成 → 不等式が満たされているペアを大量生成 → ギリギリ不等式が満たされているペアを優先採用して、車として出力、 程度のものです。これを小さい行列で作って、 この上に次元だけ拡大してsparseに不等式が壊れないようにランダムに値を増やす カモフラージュ次元増加戦略なども考えられていたのですが、 巨大すぎる燃料を作るとこっちのエンコーダが悪いのかサーバのデコーダが悪いのかうまく submit できないので小さめに抑えました。 行列ライブラリは Eigen を使ってます。 割とお気に入り。 これも、それなりに時間を掛けて探索するようにして、あとは自動サブミットスクリプトを回して頑張って貰うことに。 スクリプトで、サブミットした車IDを控えておくのを忘れたので、どれが自社製品だかわからなくなってしまった…。
そしてひたすらソルバを回し続ける。
開始69時間(Generator.java): 突然tsukunoさんが回路ゴルフに燃え始めた。 というわけで、n文字を6+3nゲートにするエンコーダから、n文字を1.66nゲートにするエンコーダに置き換え。 詳細はこちら。
Time Up
といった感じでした。
