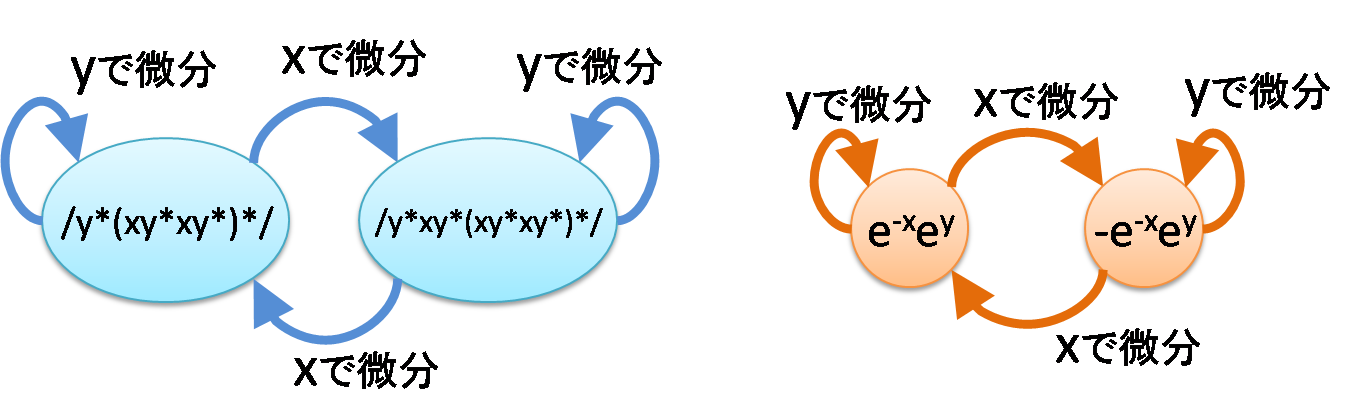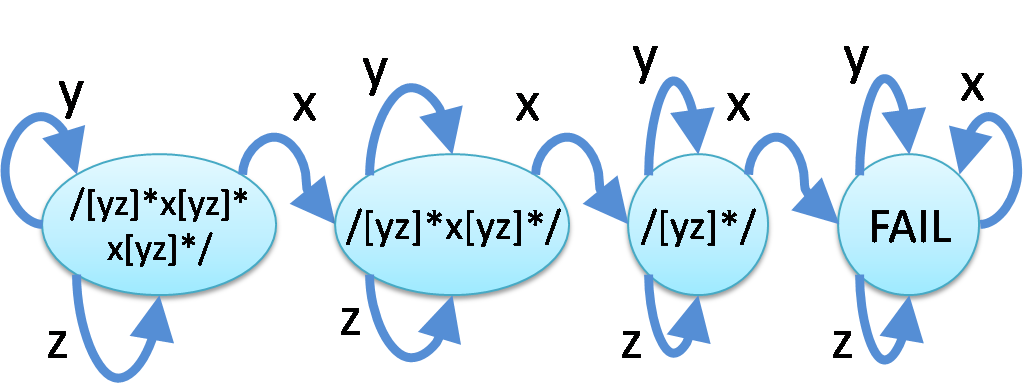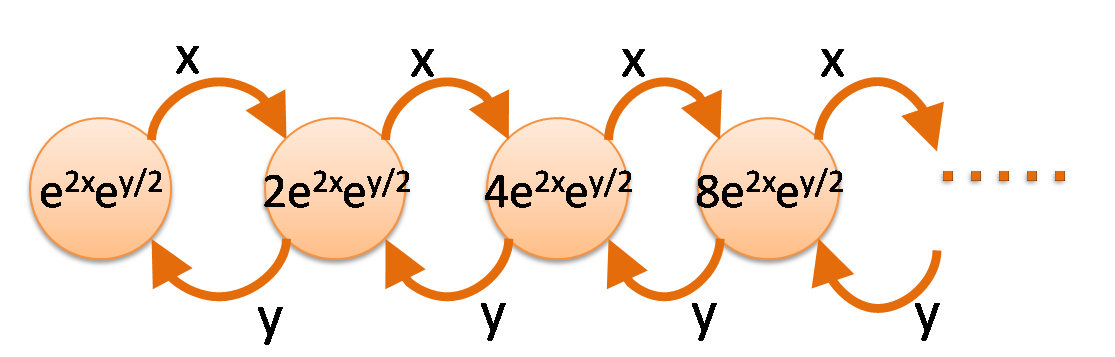00:46 10/04/23
EDBT/ICDT 2010
先月 EDBT/ICDT 2010
という学会に行ってきたのですが、それについて何も書いてなかったので今頃書きます。
自分より一ヶ月後に同じローザンヌに行って噴火に巻き込まれて帰国まで延びてしまっているみずしまさん がお帰りになるよりは早く書かないと的気分がなきにしもあらずです。
データベースの会議なんですが、
こちらの分野は SIGMOD/PODS の流れで、
実装寄りの会議と理論よりの会議を合わせて共同開催するブームらしい。
参加者としては、色んな幅広いトークが聴けるのは単純に楽しいので、もっと広まると面白そうだなあと感じました。
プログラミング言語で言うと
PLDI /POPL
とするみたいなものでしょうか。
それが良いかどうか判断できるほどPLDIの方の雰囲気を知らないのでわかりませんが。
オートマトン方面だと
CIAA /DLT
なんかはいい加減くっつけよくらい。
面白かった発表は… 基調講演・招待講演 が、どれも、
最近こっち方面で流行っているんだなーと遠目に見ていた分野をまとめてくれててわかりやすかったです。
特に、データが確率で重み付いてる感じのデータを扱う Probabilistic Database の話と、
クエリや処理を繰り返してできあがった最終データの各要素が元々のデータベースのどこから来ている、
といった情報をトレースする Provenance の話。
後者は、要はアノテーションだ、というのと、関係代数でできる最適化規則を通そうとすると、
その上に載せられるアノテーションは必然的に 半環
にならざるを得ないし、それしか仮定しなくて良い、等々、なるほどでした。
他には 併設ワークショップ で、
大規模データを公開するような場合にプライバシーを漏洩させないような適切な匿名化、
という話で、 その 「適切な」 「匿名化」 というもの自体の数学的なモデルの定義がまず問題だ、
といった辺りのお話。
理論的なトークでは、「多項式時間計算可能なクエリをすべて、そしてそれだけを書けるクエリ言語はあるか」
という長年の未解決問題へのアタックの話が楽しかった。
データベースの構造にある種の条件を課せば「ある」のだけれど、その条件をゆるめて行く試みの話で、
グラフ理論の話にもっていって、
平面グラフ
の K_3,3 と K_5 が有名ですがこういう「禁止マイナーグラフ」を持つ、
ということさえ分かっていれば上手くいくことがわかったらしい。
禁止マイナーを持つ → 平面とは限らないがなんらかの面に埋め込める →
埋め込みを利用して無理矢理データ間に順序を定義できる →
全順序のある構造なら多項式時間の特徴付けは上手くいくことがわかっている、という流れ。
グラフマイナーの理論はなんだか本当すごいなあ。全然大したことのないように見える条件から凄い物を引っ張ってくる。
23:49 10/04/02
微分と微分の話：解題
『要するに"derive your dreams"は式通りに展開すると"our dreams"になるんですね、分かります。』
@nodchip
先日の 『正規表現 ＝ 関数 』 の舞台裏です。
まず最初に感謝の言葉。
TuvianNavy さんの考察
を読んだのがすべての発想のきっかけです。 ありがとうございます。
私自身個人的には、今のところ知る/考える限りでは、
この２つの世界の 「正則」 に特に歴史的に意味のある関連はないと思っています。
しかし、このアナロジーを具体的に推し進めてみたらどこまで行けるものか、 とても面白い。 興味を持ちました。
ということで、 具体例をいくつか考えてみたのが件のテキストです。
エイプリルフールの即興ネタとして面白くするために、 綺麗にいく例ばかり集めました。
うまくないケースについては、後で紹介します。
どこからがネタ？
b:id:coleus [math][programming][research] 「本題」の部分だけエイプリルフール？ 正規表現の微分は普通に面白い。
はい。 Brzozowski の微分（"derivative": 直訳は"導関数"かな）の話は、本当にある研究の紹介です。
こちら方面の論文では十本の指に入る有名な古典…と言っても過言ではないと思う。
同じく準備の節で紹介した Antimirov の "偏微分" の論文ともども、非常に面白いので、
興味を持たれた方はぜひぜひ調べてみて下さい。
あ、もちろん 「April Baker さん」 も嘘ですよ。
「微分」なの？
xyx を x で素直に"微分"すると yx + xy になる。 単に左からけずると yx になる。微分というより、 左からの積についての割り算を定義してるだけなんじゃないのかなぁというのが第一印象でした。
@yu_sakasaki
(via @hotwatermorning )
まさに。 例の演算は、 実は
左からの商 (left quotient)
とも呼ばれています。 正確に言うと、
正規表現という"表現"のことは忘れて、純粋に、表している文字列集合に対する操作 として見るとき、
この一文字削る処理の実体は、そう、割り算です。
ただし、そのような文字列集合を表記する記法である正規表現に対する、
記法に対する記号的な操作 として左商を求める記号演算を考えると、
Leibniz 則もどきの代数法則が現れます。 たぶんこれが Brzozowski がこの名前をつけた理由の、
少なくとも一つではないかなあと想像しています。
つまり、関数 f と g の積の（変数xでの）微分 '
(f・g)' = f'・g + f・g'
に対して、正規表現 f と g の連結の（文字xでの）微分 ' は
(f・g)' = f'・g | c(f)・g'
となります。c(f) は f の "constant part" なるもので、
要は f が空文字列にマッチするなら //、しないなら FAIL です。
この c という余計なものの入った法則程度の類似性で何が言えるかというと…さて、私もよく知りません。
どうなんでしょうか。とりあえず今回は、
「同じ名前がついてるからというだけの理由で強引に同一視するネタ」
以上に特に意味はありません。
本題
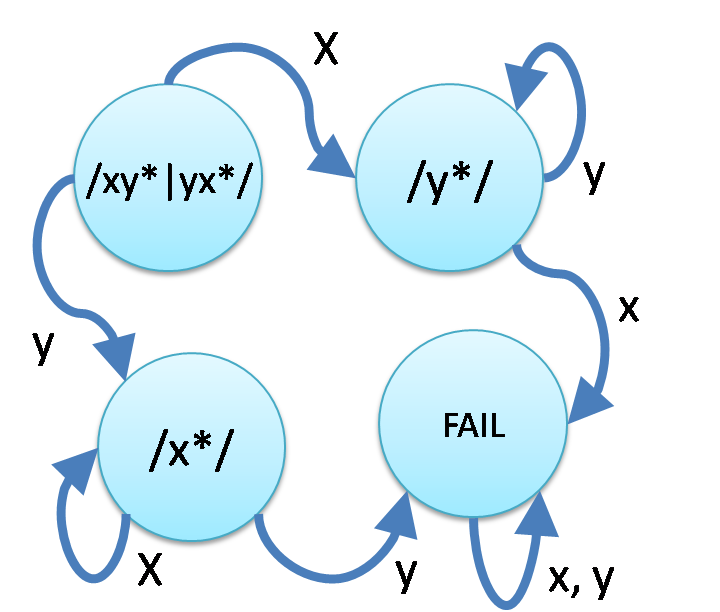
/xy*|yx*/ (左図) に対応する関数はなんでしょう？
δ/δx でも、δ/δy でも、何回でも微分できる関数であることは確かです。
C∞級 とかいう。
さてところで、二階微分が連続関数なら、
x で微分したあと y で微分しても、 逆に y で微分したあと x で微分しても、
必ず結果が等しくなるという定理 があります。
ところが！ /xy*|yx*/ を x で微分した後 y で微分した結果 /y*/
と、 y で微分した後 x で微分した結果 /x*/ は、違う正規表現です。
こんなことになる関数は存在しません。
というわけで、残念ながら正規表現の世界を関数と微分の世界に埋め込める、というのは嘘でした。 残念！
そう上手くはいきませんね。
一昨日の例はすべて、 こうならない、
「文字列をシャッフルしてもマッチする/しないが変わらない」ような正規表現だけを選んで掲載しています。
それだけ？
私が今のところ考えている範囲は、 ここまでです。はい。 猛烈にわかりにくいオチでスミマセンでした。
オチが面白くないのは、 あー微分が非可換な正規表現だと駄目だなーと思いついたのが偶然 3 月 31
日の夜だったせいでエイプリルフール化してしまったためで、
他の日なら普通の考察記事として書いていただろう内容だからなのです。
今でも、「さらに深く考えれば本当に面白いものが出てくる可能性はあるんじゃないか？」 と半分くらい思っています。
（半分は、なにか色々条件をつけてけばそりゃ当然そのうち"完全一致"する構造は見つけられるだろうけど、
それが何か面白くなってるかどうかはどうだろなー、くらい。）
そもそも、 解析や微分や偏微分なんてもうほとんど覚えてないので、
自分で自分の疑問にまったく答えられないのが厳しい。
「じゃ、文字列をシャッフルしてもマッチが変わらない正規表現だけに限定すれば
必ず対応する関数は見つけられるのか？」
「正規表現のオートマトンの形から、 対応する関数の満たすべき線形偏微分方程式系が作れるけど、
これって解の存在性とか公式の存在とかってどうだったっけ？」
「実数や複素平面の上の関数の微分だけじゃなくて、
なんかもっと一般の多様体にならC∞級だけど非可換な微分ってあったりするんだっけ？」
数学力が足りない…。
21:59 10/04/01
現代将棋の世界にこんにちは
* ---- K-Shogi V2.7.00 棋譜ファイル ----
開始日時：2010/04/01(木) 19:23:10
終了日時：2010/04/01(木) 21:55:22
手合割：平手
先手：挨拶六段
後手：世界八段
▲５六歩 △５四歩 ▲５五歩 △同 歩 ▲９六歩 △９四歩
▲９八香 △９五歩 ▲同 歩 △９二香 ▲５六歩打 △同 歩
▲５八玉 △９七歩打 ▲同 香 △９六歩打 ▲同 香 △９五香
▲５七歩打 △９六香 ▲５六歩 △５二金左上▲５五歩 △５三金
▲５四歩 △同 金 ▲９九歩打 △５三金 ▲９八歩 △５四金
▲９七歩 △５三金 ▲９六歩 △５四金 ▲９五歩 △５三金
▲９四歩 △５四金 ▲９三歩成 △５三金 ▲９二と △５四金
▲９一と △５三金 ▲９二と △５四金 ▲９三と △５三金
▲９四と △５四金 ▲９五と △５三金 ▲９六と △５四金
▲９七と △５三金 ▲９八と △５四金 ▲９九と △９六歩打
▲９八と △５三金 ▲９七と △５四金 ▲９六と △５三金
▲５四歩打 △９五歩打 ▲５九玉 △５二金引 ▲５三歩成 △同 金
▲５七歩打 △５四金 ▲５六歩 △９三桂 ▲９五と △９四香打
▲５八玉 △９五香 ▲５九玉 △５三歩打 ▲５八玉 △５五金
▲同 歩 △５四歩 ▲同 歩 △５二歩打 ▲５三歩成 △同 歩
▲９九歩打 △５四歩 ▲９八歩 △５五歩 ▲９七歩 △５六歩
▲５二金打 △同 玉 ▲９六香打 △６二銀 ▲６八金 △５一金
▲５七金 △７一銀 ▲５六金 △６一金 ▲５九玉 △９六香
▲同 歩 △６二銀 ▲５八歩打 △４二銀 ▲４六金 △５三銀左上
▲５七歩 △５八金打 ▲同 玉 △９一香打 ▲５四金打 △４二銀
▲５六金 △９二香 ▲５九玉 △５三歩打 ▲５八玉 △３一銀
▲９五歩 △４二銀 ▲４六金 △３一銀 ▲９四歩 △４二銀
▲９三歩成 △同 香 ▲５六金 △９四香 ▲５九玉 △５四歩
▲９五歩打 △８四歩 ▲５八金 △９五香 ▲４八金 △９六香
▲５八玉 △５一金 ▲５三桂打 △同 玉 ▲９七香打 △同 香成
▲７六歩 △４一香打 ▲７七桂 △６一金 ▲４六歩 △３一銀
▲６六歩 △４二銀 ▲６五桂 △４四玉 ▲４五金 △投了
まで161手で先手の勝ち
ModanShogi
の Strict モードで "Hello, world!\n" を出力するプログラムを書いてみました。
せっかくなので、出力が終わった次の一手で詰ませて終わるようにしてあります。
ただし、一カ所VMの実装が気に入らなかったので勝手に変更してしまいました。
桂馬を使うと（割り切れる場合でも）値が Float になって以降文字出力できなくなってしまうのが悲しいので、
出力の際には整数に戻すように…
*** lib/shogimodan/orig-vm.rb Wed Mar 31 19:25:40 2010
--- lib/shogimodan/vm.rb Thu Apr 01 22:05:55 2010
***************
*** 47,55 ****
set(arg1, val)
when :putc
if defined?(Encoding) then
! @stdout.print get(arg1).chr(Encoding::UTF_8)
else
! @stdout.print get(arg1).chr
end
when :jump_if
if get(arg1) != 0
--- 47,55 ----
set(arg1, val)
when :putc
if defined?(Encoding) then
! @stdout.print get(arg1).to_i.chr(Encoding::UTF_8)
else
! @stdout.print get(arg1).to_i.chr
end
when :jump_if
if get(arg1) != 0
こうなっていなくても特に困らないのですが、桂馬が事実上使用禁止になってしまうよりは、
こうした方が美しいと思うので。
自動化もしくはゴルフは他の方に任せる。
追記
04:01 10/04/01
関数と正規表現と私
April Baker さんの "Analysis and Regex" という論文が面白かったので紹介しようと思います。
例えば 「λ計算と論理学の証明には一対一の対応がつく！ 」 のような、
一見ちょっと全然違いそうなものに実は重大な対応関係が…という発見はとても楽しいものですが、
今回のこれもそんなお話です。曰く、「正規表現には、
解析関数（sin とか cos とか exp とか…）が対応する！」
準備A
前提知識として、J. Brzozowski "Derivatives of Regular Expressions" という研究があります。
これは、正規表現に対する「微分」という演算を考えてみると面白いんじゃね？という。
/x(x|y)*x/ を x で微分すると /(x|y)*x/
（※以下では、「マッチする」というのを、文字列全体 が正規表現に適合する、という意味で使います。
なので Perl などの表記に正確に書くと、ここは /^x(x|y)*x$/ を x で微分すると /^(x|y)*x$/、
と書くべきところですけど面倒なので略記。）
正規表現 r を文字 c で微分すると、「c の後ろにくっつけたら r にマッチするようになる文字列全部、
にマッチする正規表現」を返すというのが定義です。この例だと、'x' の後ろには "xxx" や "xyxyx" や
"x" や "yyyyyyx" をくっつけると /x(x|y)*x/ にマッチするようになるので、
そういうの全部を拾えるパターンは /(x|y)*x/ です。
/(x|y)*x/ を y で微分すると /(x|y)*x/
こんな風に、微分してもパターンが変わらないこともあります。/(x|y)*x/ にマッチする文字列は、
どれも 'y' の後ろにくっつけたら、また /(x|y)*x/ にマッチするので変わりません。
/(x|y)*x/ を x で微分すると /(x|y)*x|/
xで微分した場合は、わかりにくいですが、最後１文字だけ違います。
'x' の後ろに空文字列 "" をくっつけても /(x|y)*x/
にマッチするので、微分後の正規表現も、空文字列を含むようになってます。
/x(x|y)*x/ を y で微分すると FAIL
'y' の後ろに何をくっつけても /x(x|y)*x/ にマッチするようにはならないので、
この場合は、どんな文字列にも絶対マッチしない特別な正規表現(?)オブジェクトを返します。
このオブジェクトは FAIL と書くことにします。
準備B
この演算をなぜ「微分」と呼ぶかというと、| を足し算、正規表現の連結を掛け算と見立てると、
高校数学に普通にでてくるような関数の和の微分や積の微分の公式によく似た式が成立するからなんですが、
まあ、今回はその辺はどうでもいいです。
Brzozowski の論文は、「正規表現を微分した結果はまた必ず正規表現で書ける文字列集合になること」を示し、
「正規表現の式の形から機械的に微分を求める、要するに"公式"」を明らかにしたことと、そして
「１個の正規表現から始めて微分を繰り返しまくっても、出てくるパターンは有限しかない
（無限に新しいパターンが出てきたりはしない）」ことを明らかにしたものです。これらの性質を使うと、
微分演算によって、正規表現マッチの実行に必要な「オートマトン 」を作り出せたりします。
教科書にはあんまり載っていないですが、この微分によるオートマトンの作り方は結構意外と効率的だったりするらしい。
[Antimirov 95]
などがこの方向の発展研究です。
本題
Brzozowski 微分の性質で特に重要なのは 「微分で出てくるパターンは有限しかない」 ところです。
有限しかない、ってどういうことでしょう？ 絵で描いてみるとよくわかります。
一番パターンが少ない例で考えてみましょう。
/x*/ という正規表現は、x で何回微分しても元の /x*/ のまま変わりません。
なので、ぐるぐるとループして、パターンは１個しか出てきません。
指数関数
です。自然対数の底 e の指数関数は、微分すると全く同じ自分自身に戻ります。
つまり、「微分」という観点だけ で抽象化して見るならば、/x*/ は e^x
と全く同じもの
アイデアはこれだけです。簡単ですね。この「微分」の目を通して、
どんな正規表現も関数の世界に埋め込んでしまいましょう。次はもう少し複雑な例です。
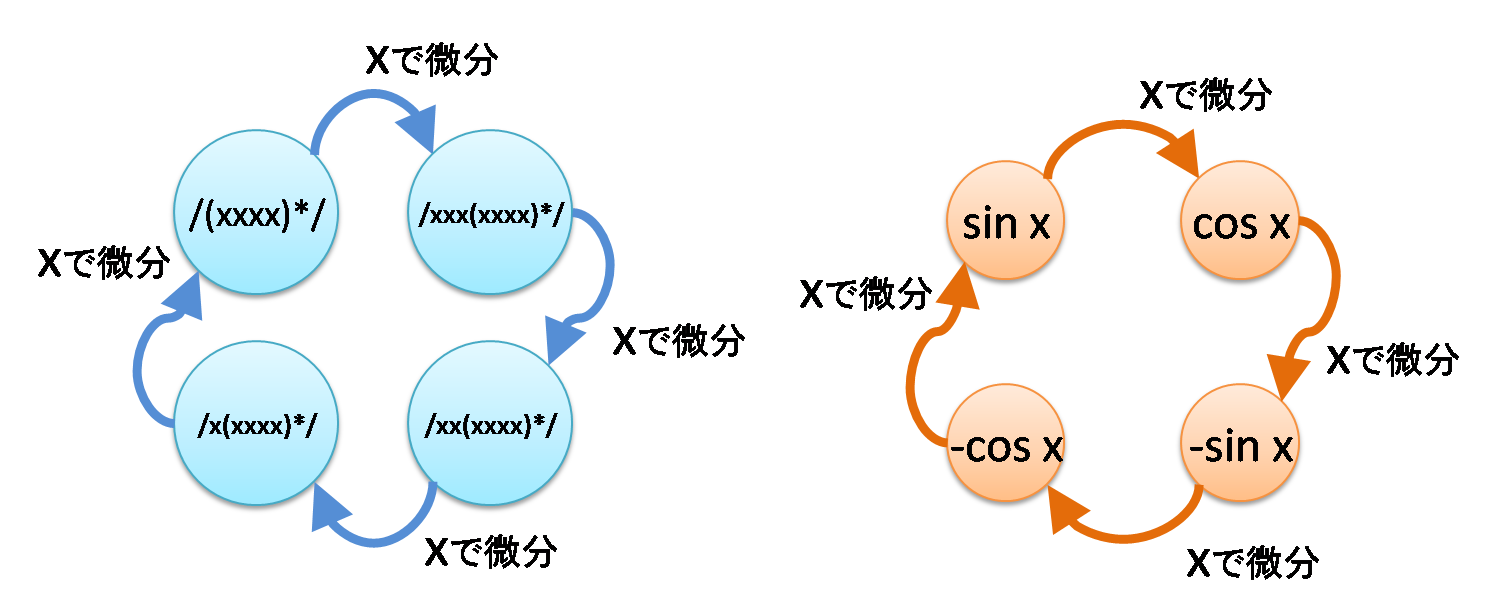
/(xxxx)*/、xが4の倍数個並ぶ、という正規表現は、一回微分すると…
「'x'の後ろにつなげたらxの個数が4の倍数になる文字列」になるはずなので、つまり
4で割って3余る個数xが並んだ文字列にマッチする正規表現です。同じ議論を繰り返すと…
対応する物は、４回微分すると元に戻ってくる、sin(x) なのでした！
いろんな例
文字の種類というか変数の種類が１種類だとつまらないですね。
２種類に増やしましょう。/y*(xy*xy*)*/ という、
偶数個のxでyが区切られてる文字列にマッチする正規表現。'x' を ',' と思うと、
奇数個カラムがあるCSVか何かです、きっと。これは、
微分すると２個のパターンが現れます（本当かどうか気になる方は検算してみて下さい）。
文字の種類＝微分の種類が x と y の２種類に増えたので、関数の世界でも、二変数の関数と、偏微分δ/δx, δ/δyを考えます。
今回、微分の作る構造が全く同じな関数は、e^-x e^y です。
さらに３変数でも４変数でも同じように一般化できます。もひとつ例出しときましょう。
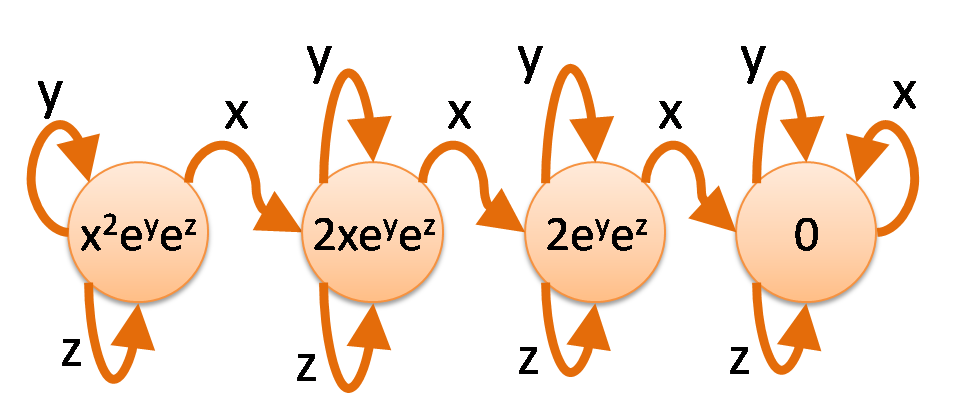
さっきまでは * でループするような正規表現ばっかり出してきましたが、たとえば
/[yz]*x[yz]*x[yz]*/ つまり「xをちょうどピッタリ２個含む」のようなループしてない要素を含む表現だと、
指数関数ではなくて、多項式関数が出てくるみたいですね。
なにが嬉しいの？
こんな奇妙な、正規表現の別の表し方を考えると、何が一体嬉しいんでしょうか？
ちょっと逆説的ですが、これは、「正規表現で書けないもの」についてもナチュラルに思いを馳せることができるところです。
たとえば、「xとyがちょうど同じ回数でてくる文字列」というパターンは、正規表現では書けません
（Perlとかのスーパー拡張正規表現では書けるかもしれませんが、そういうのは抜きで）。
何故書けないとわかるかというと、微分してみると「xよりyの方が1個多い文字列」「xよりyの方が2個多い文字列」
「同3個多い文字列」…と、無限にパターンが出てしまうからです。
こういうパターンを扱うには、正規表現から根本的にステップアップした
文脈自由文法
や
プッシュダウン・オートマトン
のような道具を持ち出す必要がありました。
ところが、最初から、正規表現ではなく関数の微分の世界で考えていたらどうでしょう。
さっき出てきたような指数関数を、ちょっとパラメタを変えるだけで、
「xとyがちょうど同じ回数でてくる文字列」
の無限の微分構造と対応する関数が得られます。
e^{2x} e^{y/2} の微分には無限個のパターンがありますが、しかし、
x と y でちょうど同じ回数ずつ偏微分したときだけ元の関数に戻ります。まさに求めていた物です。
さらにもうちょっと変えるだけで、e^{2x} e^{3y} e^{z/6} なら、
文脈自由文法すら越える「xとyとzがどれも同じ個数出てくる文字列」を捉えることができちゃいます。
と、こんな風に、強力な文法を考えるたびにナントカオートマトンを持ち出す必要がなく、
すべて、関数とその微分、という表現で、
関数のパラメタをちょこちょこ変えるだけで統一的に表現できてしまうのです。面白いですね！
※ 追記
以上の記事は、エイプリルフールの嘘ネタです。 謝辞・ネタばらし・マジ部分の補足などは 後日の解説 をご覧下さい。
それで本題の「正規表現の微分構造は、数学の関数に対応する！」 という話題なんですが、
どこまで本当なんでしょうか。
と、準備が終わったので、元の話に戻りましょう。なんでしたっけ。ええと、
April Baker さんの、「正規表現は数学関数！！！」というお話です。
ところでですね、いちど正規表現のことは忘れて「微分しても元と変わらない」という文言にだけ着目して下さい。
……「微分」という言葉の本来の出所、関数の微分についてご存じの方は、
全く同じ言葉が出てきたことを思い出されるのではないでしょうか？
そう、
