letsboost::graph

sample

サンプルの動作確認バージョン [GCC4.4/1.41.0] [VC9/1.41.0]

#include <iostream>
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/graph/visitors.hpp>
#include <boost/graph/graph_utility.hpp>

using namespace std;
using namespace boost;


typedef adjacency_list< vecS, vecS, directedS,
	no_property,
	property<edge_weight_t, int>
> Graph;

typedef graph_traits<Graph>::vertex_descriptor
  Vertex;

typedef pair<int,int>
  Edge;


int main()
{
	// 辺のリスト
	Edge links[] = {
		Edge(0,1), Edge(0,2),
		Edge(1,2), Edge(1,4),
		Edge(2,0), Edge(2,3),
		Edge(3,4),
	};
	// 各辺の距離
	// （ここを変えることで0と1の間が遠くて2と3が近い、
	// 　みたいなことも表現できます。）
	int weights[] = {
		1, 1,
		1, 1,
		1, 1,
		1,
	};
	const size_t nEdges = sizeof(links)/sizeof(*links);

	// ５点のグラフを構築
	Graph g( links, links+nEdges, weights, 5 );

	Vertex p[5] = {0};

	// 始点を点0にしてdijkstraのアルゴリズムを実行。
	// # 点0から点iに最短経路で行くには、点iの前に点p[i]
	// # に行ってそこからiに進めばよい、という情報が入る。
	Vertex s = 0;
	dijkstra_shortest_paths( g, s,
		visitor( make_dijkstra_visitor (
		record_predecessors( p, on_edge_relaxed() )
	)));

	cout << "shortest paths tree" << endl;

	// 結果の表示
	adjacency_list<> tree(5);
	graph_traits<Graph>::vertex_iterator vi, vend;
	for( tie(vi,vend) = vertices(g); vi!=vend; ++vi )
		if( *vi != p[*vi] )
			add_edge( p[*vi], *vi, tree );

	print_graph(tree);

	return 0;
}

出力例

0 --> 1 2
1 --> 4
2 --> 3
3 -->
4 -->

要するに、0 から始まる最短ルートは

0 -- 1
0 -- 2
0 -- 2 -- 3
0 -- 1 -- 4

であることがわかります。0 -- 2 -- 3 -- 4 などは長いのでダメ、と。

etc

グラフ理論に詳しい方にはお馴染みかと思われるアルゴリズムの集合です。関数の名前を挙げていくと depth_first_search, breadth_first_visit, dijkstra_shortest_path, johnson_all_pairs_shortest_paths, prim_minimum_spanning_tree, edmunds_karp_max_flow などなどなどなど。グラフの情報を保持するデータ構造として、隣接行列による表現や、隣接リストによるものを用いることが出来ます。

グラフについて

このライブラリ、その筋の人でないと何をするものなのかさっぱりわからないと思いますので、ここで多少の解説を試みます。グラフというのは、例えば二分木とかの「木」をもっと一般化したデータ構造で、点とその間の接続関係（辺）から成り立っています。例えば上のサンプルで使ったグラフを絵にすると、下のような感じ。

説明の図

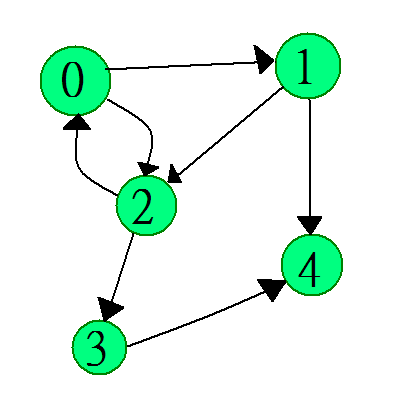
で、グラフが与えられたときに、「この点からこの点の最短経路を求める」とか「どこかにループがあるかどうか調べる」といったアルゴリズムが色々知られていて、分野によってはかなり便利に使うことが出来ます。

実際の利用例としては、例えば「複数のソースファイルの依存関係をグラフで表して、どの順番でコンパイルすればＯＫなのか調べる」とか、「地図の色の塗り分け方（隣り合う国は違う色で塗る）でできるだけ色数を少なくできるものを探す」とか「ウェブページどうしのリンク関係をグラフで表して、 PageRankを計算する」とか「鉄道の路線図をグラフで表して最短経路を求める」など。

詳しく調べてみたい方には、『レナのふしぎな数学の旅』という入門書がおすすめです。

boost::graph

abstract

sample

出力例

etc

グラフについて

see also